Why $\cos(-\theta)$ gives positive values while in case of sine it is negative?

Question

Why $\cos(-\theta)$ gives positive values while in case of sine it is negative?

I mean

$\cos(-\theta) = +\cos(\theta)$

$\sin(-\theta) = -\sin(\theta)$

$\tan(-\theta) = -\tan(\theta)$

and please explain General Angles in simple worlds?

Answer 1

Changing the sign of $\theta$ corresponds to going around in the other direction. Because $\theta$ is measured from the positive $x$-axis, all this does is to flip the endpoint over the $x$-axis, as shown below.

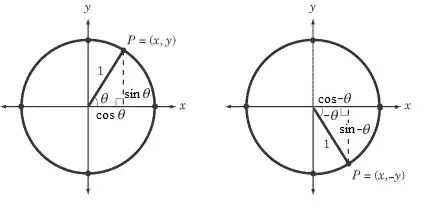
Since cosine is the $x$-component of $P$, and sine is the $y$ component, flipping over the $x$-axis will negate $\sin \theta$, but not $\cos \theta$. Hopefully this makes it clear why sine and cosine behave the way they do.

With tangent, just recall that $\tan \theta = \frac{\sin \theta }{\cos \theta }$, and since only one part of the fraction gets a $-$ sign, the tangent gets one as well.

Answer 2

The series expansipns of cos and sin are:

$cos (x)= \sum_{n=0}^\infty\frac {(-1)^nx^{2n}}{(2n)!}=1-x^2/2+x^4/4!\pm...$ and

$sin (x)= \sum_{n=0}^\infty\frac {(-1)^nx^{2n+1}}{(2n+1)!}=x-x^3/3!+x^5/5!\pm...$

Notoce here that changing the sign for cos makes no difference, (as we have all even powers of x) but changing the sign for sin does (since we have all odd powers of x).

Also $\tan (-\theta)=\frac {sin (-\theta)}{cos (-\theta)}\frac {-sin (\theta)}{cos (\theta)}=-tan (\theta)$.

Answer 3

A function $f(x)$ is said to be even, if $f(-x) = f(x)$. On the other hand a function $g(x)$ is said to be odd, if $g(-x) = -g(x)$. Thus we want to know why $cos(x)$ an even function while $sin(y)$ is odd. Now we can visualize how sine and cosine vary with angle theta ($θ$) using a unit circle in Cartesian coordinates. Draw any radius of the unit circle, making an angle of $θ$ with the positive half of the x-axis. The point on the circle where this radius intersects will have the x and y-coordinates as $\cos(θ)$ and $\sin(θ)$, respectively. This is a natural consequence of hypotenuse of the corresponding right triangle being 1 (any radius of unit circle will by definition be 1). Radius of unit circle as hypotenuse of right triangle Now as we change the angle $\theta$ we get various values of $sinθ$ and $cosθ$. These have been potted on the following graph: Graphs of $\cos(x)$ and $\sin(y)$

As you can see the graph of cosine is symmetric about the y-axis which means that for each $x$, $\cos(x) = \cos(-x)$. Making cosine an even function. On the other hand if you look at graph of sine, you would notice $|\sin(x)|$ = $|\sin(-x)|$ but sign is opposite. That is absolute value is same as we cross the $y$-axis but direction is reversed. Making sine an odd function.

Answer 4

Trigonometric functions were introduced to do computations about triangles. Consider the following picture:

cosine law 1

and set $a=BC$, $b=AC$, $c=AB$. Set also $h=CH$ and $d=AH$. Then you can say $$ b^2=d^2+h^2,\qquad a^2=(c-d)^2+h^2. $$ If we subtract the two equalities, we get $$ b^2-a^2=d^2-(c-d)^2=-c^2+2cd $$ or $$ a^2=b^2+c^2-2cd. $$ But now, by definition, $d=b\cos\alpha$, so we obtain the cosine law for acute angles.

In ancient times sines and cosines were not attributed a “sign”; they were just defined with ratios using right triangles, so they made sense only for acute angles. For an obtuse triangle the figure is

Cosine law 2

With the same notation as before, we get the relations $$ b^2=d^2+h^2,\qquad a^2=(c+d)^2+h^2 $$ and subtracting gives $$ b^2-a^2=d^2-(c+d)^2=-c^2-2cd $$ or $$ a^2=b^2+c^2+2cd. $$ Now, if $\bar\alpha$ denotes the supplementary angle of $\alpha$, we can write the cosine law for obtuse triangles: $$ a^2=b^2+c^2+2bc\cos\bar\alpha. $$ When negative numbers became less suspicious, people started to realize that one could define the cosine of an obtuse angle as the negative of the cosine of the supplementary angle, so that only one cosine law could be written: $$ a^2=b^2+c^2-2bc\cos\alpha. $$ A similar reasoning based on the sine law makes it clear that the sine of an obtuse angle should be the same as the sine of the supplementary angle.

Sines and cosines were later defined for any angle; the extension can be justified with the trigonometric circle and it became clear that one had to define them so that $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\alpha $$ just by looking at the trigonometric circle.

Answer 5

$\cos(-\theta)=\cos(0-\theta)=\cos0\cos\theta+\sin0\sin\theta=\cos(\theta)$.

$\sin(-\theta)=\sin(0-\theta)=\sin0\cos\theta-\cos0\sin\theta=-\sin(\theta)$.

$\tan(-\theta)=\frac {\sin(-\theta)}{\cos(-\theta)}=-\tan(\theta)$.(Using above two equalities.)

Answer 6

Well cosine takes values from 1 to -1 in interval of $[0,\pi]$ while sine takes values from 0 to 1. I don't know what you mean by General Angles in simple words.

Answer 7

Trigonometric functions were introduced to do computations about triangles. Consider the following picture:

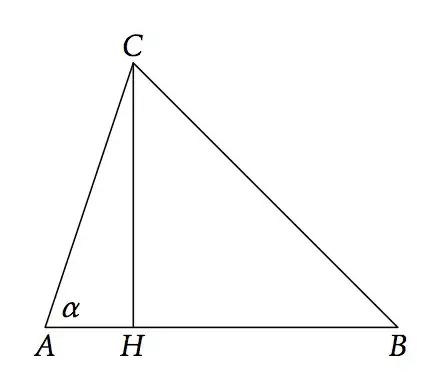
and set $a=BC$, $b=AC$, $c=AB$. Set also $h=CH$ and $d=AH$. Then you can say $$ b^2=d^2+h^2,\qquad a^2=(c-d)^2+h^2. $$ If we subtract the two equalities, we get $$ b^2-a^2=d^2-(c-d)^2=-c^2+2cd $$ or $$ a^2=b^2+c^2-2cd. $$ But now, by definition, $d=b\cos\alpha$, so we obtain the cosine law for acute angles.

In ancient times sines and cosines were not attributed a “sign”; they were just defined with ratios using right triangles, so they made sense only for acute angles. For an obtuse triangle the figure is

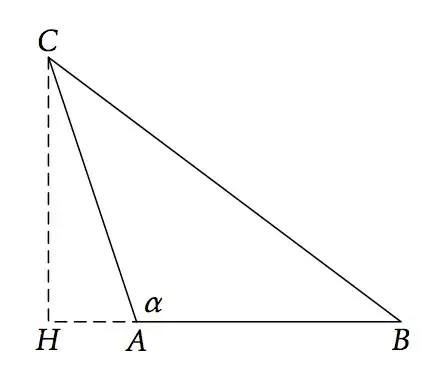
With the same notation as before, we get the relations $$ b^2=d^2+h^2,\qquad a^2=(c+d)^2+h^2 $$ and subtracting gives $$ b^2-a^2=d^2-(c+d)^2=-c^2-2cd $$ or $$ a^2=b^2+c^2+2cd. $$ Now, if $\bar\alpha$ denotes the supplementary angle of $\alpha$, we can write the cosine law for obtuse triangles: $$ a^2=b^2+c^2+2bc\cos\bar\alpha. $$ When negative numbers became less suspicious, people started to realize that one could define the cosine of an obtuse angle as the negative of the cosine of the supplementary angle, so that only one cosine law could be written: $$ a^2=b^2+c^2-2bc\cos\alpha. $$ A similar reasoning based on the sine law makes it clear that the sine of an obtuse angle should be the same as the sine of the supplementary angle.

Sines and cosines were later defined for any angle; the extension can be justified with the trigonometric circle and it became clear that one had to define them so that $$ \sin(-\alpha)=-\sin\alpha,\qquad \cos(-\alpha)=\cos\alpha $$ just by looking at the trigonometric circle.

Answer 8

Remember, that angles are measured from the positive $x$-axis. Draw a line to form an angle $\theta$ with the positive $x$-axis. This line has intersects the unit circle at $(\cos\theta,\sin\theta)$ and has equation $y=x\tan\theta$.

For the angle $\alpha=-\theta$, everything is mirrored around the $x$-axis. The reflection of a point $(x,y)$ about the $x$-axis is the point $(x,-y)$. The reflection of our original line about the $x$-axis will therefore cross the unit circle at $(\cos\theta,-\sin\theta)$ and have formula $y=-x\tan\theta$.

So if the line forming the angle $\alpha$ intersects the unit circle at $(\cos\alpha,\sin\alpha)$ and has equation $y=x\tan\alpha$, we have

$$\cos\alpha=\cos(-\theta)=\cos\theta$$ $$\sin\alpha=\sin(-\theta)=-\sin\theta$$ $$\tan\alpha=\tan(-\theta)=-\tan\theta$$