2

The black line represents the xis of the cone and theta is the maximum angle

My question is pretty much the same as this question below, however I came up with a potential solution to this problem that I didn't see an answer to in the other question and I was wondering if it is a viable answer.

Generate a random direction within a cone

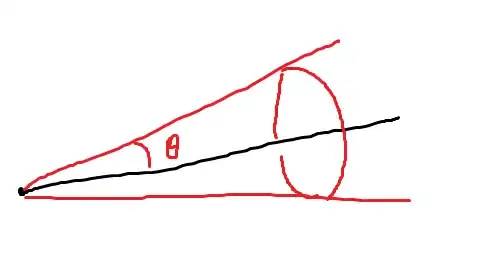
If you didn't open the link, basically you have a cone oriented along the black line and I want to generate a uniformly sampled vector within the cone.

I was thinking I could do the following:

1) Normalize the axis of the cone (black line) and call it N

2) Generate a uniformly distributed vector R within the hemisphere centered around N using this code: http://pathtracing.wordpress.com/2011/03/03/cosine-weighted-hemisphere/ Note: Not sure if cosine-weighted or unweighted sampling would be better

3) Check to see if the angle between N and R is less than the cone's theta

4) If it's less, we're done and we have our angle. If not, go back to step 2 and repeat.

Also, I would like to calculate the PDF of this conal distribution. According to a lecture slide of a class I once took a while back, the probability of choosing any given direction within the cone is as follows:

$p = \frac {1}{2\pi(1 - \cos\theta)}$

I was wondering if this probability is 1) accurate and 2) still holds true with my potential method above.

Community
  • 1
user1855952
  • 443

1 Answers1

1

To check the accuracy, you should integrate the pdf through the cone and get 1, also the accuracy of your approximation depends on how good the normal distribution is, since the symmetry of the cone should mean that a normal distribution is valid.

Ellya
  • 11,783