Existence of least squares solution to $Ax=b$

Question

Does a least squares solution to $Ax=b$ always exist?

Answer 1

If you think at the least squares problem geometrically, the answer is obviously "yes", by definition.

Let me try to explain why. For the sake of simplicity, assume the number of rows of $A$ is greater or equal than the number of its columns and it has full rang (i.e., its columns are linearly independent vectors). Without these hypotheses the answer is still "yes", but the explanation is a little bit more involved.

If you have a system of linear equations

$$ Ax = b \ , $$

you can look at it as the following equivalent problem: does the vector $b$ belong to the span of the columns of $A$? That is,

$$ Ax = b \qquad \Longleftrightarrow \qquad \exists \ x_1, \dots , x_n \quad \text{such that }\quad x_1a_1 + \dots + x_na_n = b \ . $$

Here, $a_1, \dots , a_n$ are the columns of $A$ and $x = (x_1, \dots , x_n)^t$. If the answer is "yes", then the system has a solution. Otherwise, it hasn't.

So, in this latter case, when $b\notin \mathrm{span }(a_1, \dots , a_n)$, that is, when your system hasn't a solution, you "change" your original system for another one which by definition has a solution. Namely, you change vector $b$ for the nearest vector $b' \in \mathrm{span }(a_1, \dots , a_n)$. This nearest vector $b'$ is the orthogonal projection of $b$ onto $\mathrm{span }(a_1, \dots , a_n)$. So the least squares solution to your system is, by definition, the solution of

$$ Ax = b' \ , \qquad\qquad\qquad (1) $$

and your original system, with this change and the aforementioned hypotheses, becomes

$$ A^t A x = A^tb \ . \qquad\qquad\qquad (2) $$

EDIT. Formula (1) becomes formula (2) taking into account that the matrix of the orthogonal projection onto the span of columns of $A$ is

$$ P_A = A(A^tA)^{-1}A^t \ . $$

(See Wikipedia.)

So, $b' = P_Ab$. And, if you put this into formula (1), you get

$$ Ax = A(A^tA)^{-1}A^tb \qquad \Longrightarrow \qquad A^tAx = A^tA(A^tA)^{-1}A^tb = A^tb \ . $$

That is, formula (2).

Answer 2

Assume there is an exact solution $\small A \cdot x_s = b $ and reformulate your problem as $\small A \cdot x = b + e $ where e is an error ( thus $\small A \cdot x = b $ is then only an approximation as required) we have then that $\small A \cdot (x_s - x) = e $

Clearly there are arbitrary/infinitely many solutions for x possible, or say it even more clear: you may fill in any values you want into x and always get some e. The least-squares idea is to find that x such that the sum of squares of components in e ( define $\small \operatorname{ssq}(e) = \sum_{k=1}^n e_k^2 $) is minimal. But if our data are all real data (what is usually assumed) then the smallest possible sum of squares of numbers is zero, so there in fact exists an effective minimum for the sum.
Then restrictions on x may cause, that actually the error ssq(e) is bigger but always there will be a minimum $\small \operatorname{ssq}(e) \ge 0 $.

So the question is answered in the affirmative.

(A remaining question is, whether it is unique, but that was not in your original post.)

Answer 3

We just need to prove that the rank of matrix $A^TA$ equals the rank of augmented matrix $[A^TA,A^Tb]$. We prove it below:

denote the rank of matrix as rank A=k. By using the rank equality(can be found in nearly every algebra textbook.):rank $A^TA$=rank $A$=rank $A^T$. We know rank $[A^TA,A^Tb]\ge$rank A, since the former has one more column than the latter. But, on the other hand, $[A^TA,A^Tb]=A^T[A,b]$, and by using the rank inequality(can be found in some algebra textbooks): rank $AB\le$ min{rank A, rank B}. so rank $A^T[A,b]$$\le$rank $A^T$=rank A=k. Combining the two inequality, we have rank $[A^TA,A^Tb]$=k.

So the rank of matrix$[A^TA]$ is always equal to the rank of the augmented matrix$[A^TA,A^Tb]$. By the theorem of existence and uniqueness of vector equation, we know the least square problem always has at least one solution. Thus we finish our proof. Q.E.D.

Answer 4

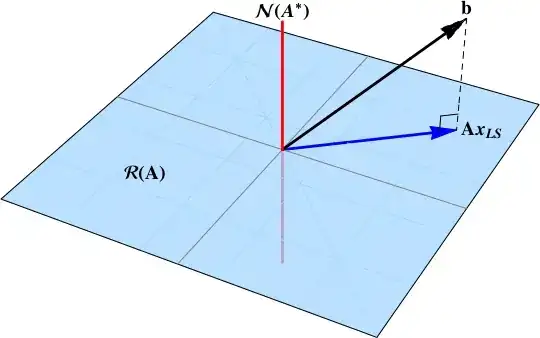
**Trivial solution only **

There is only a trivial solution when $b \in\mathcal{N}(\mathbf{A}^{*})$.

In essence, the method of least squares find the projection of the data vector $b$ onto $\mathcal{R}(\mathbf{A})$. When the data vector lives in the null space, there is no projection onto the range.

$$ \begin{align} \mathbf{A} x & = b \\ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array} \right] \left[ \begin{array}{c} x_{1} \\ x_{2} \\ \end{array} \right] &= \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] \end{align} $$

Answer 5

To see that a solution always exists, recall that the definition of a least-squares solution is one that minimizes $\|Ax-b\|_2$. To get the solution, you'd use something like the pseudoinverse on paper or some nice minimization algorithm in practice. We don't even need to refer to the rank of the matrix or anything like that to assertain the existance of a solution. Minimizing $\|Ax-b\|_2$ in $x$ amounts to minimimizing a nonnegative quadratic equation in $n$ variables (the $x_i$'s). Simple calculus alone justifies the existence of a minimum.

Answer 6

$\newcommand{\angles}[1]{\left\langle #1 \right\rangle}% \newcommand{\braces}[1]{\left\lbrace #1 \right\rbrace}% \newcommand{\bracks}[1]{\left\lbrack #1 \right\rbrack}% \newcommand{\dd}{{\rm d}}% \newcommand{\isdiv}{\,\left.\right\vert\,}% \newcommand{\ds}[1]{\displaystyle{#1}}% \newcommand{\equalby}[1]{{#1 \atop {= \atop \vphantom{\huge A}}}}% \newcommand{\expo}[1]{\,{\rm e}^{#1}\,}% \newcommand{\ic}{{\rm i}}% \newcommand{\imp}{\Longrightarrow}% \newcommand{\pars}[1]{\left( #1 \right)}% \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\pp}{{\cal P}}% \newcommand{\sgn}{\,{\rm sgn}}% \newcommand{\ul}[1]{\underline{#1}}% \newcommand{\verts}[1]{\left\vert #1 \right\vert}% \newcommand{\yy}{\Longleftrightarrow}$$\displaystyle{A^{\dagger}Ax = A^{\dagger}b}$ is equivalent to minimize $\displaystyle{\left(Ax - b\right)^{2}}$.

$\large{\sf Example}:$ $2x = 5$ and $3x = 7$ becomes $$ {2 \choose 3}\pars{x} = {5 \choose 7} \quad\imp\quad \pars{2 \quad 3}{2 \choose 3}\pars{x} = \pars{2 \quad 3}{5 \choose 7} \quad\imp\quad \pars{13}\pars{x} = \pars{31} $$

$$ x = {31 \over 13} $$ which is the minimum of the function $\pars{2x - 5}^{2} + \pars{3x - 7}^{2}$.

Answer 7

I do not think it is true because solving finding a least squares solution amounts to solving A^{T}Ax=A^{T}b, and that A^{T}A might not always be invertible. If A^{T}A is not invertible it follows, from the invertible matrix theorem, that the transformation it represents is neither onto nor one-to-one .