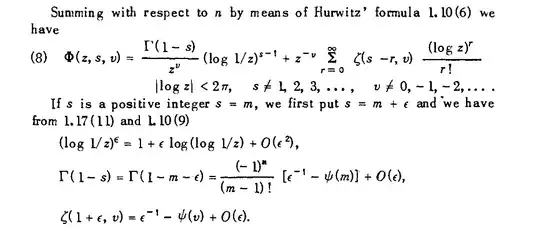Interesting question!
Your initial function is minus the Dirichlet $\eta$ function :
$$\tag{1}-\eta(s)=\left(2^{1-s}-1\right)\zeta(s)$$
Let's see what we can do with the function you obtained (for $s$ not integer) :
$$\tag{2}f(s):=\sum\limits_{k=0}^{\infty}\frac{(\pi i)^k}{k!}\zeta(s-k)$$
One problem with your derivation is that in your third equality $\,\displaystyle\frac{1^k}{1^s}+\frac{2^k}{2^s}+\frac{3^k}{3^s}+\cdots\;$ will be infinite for $k\ge s\;$ while the initial sum was convergent for $s>0$ making the equality (the exchange of sum order) problematic.
But a correct expression may be found. First some initial 'guesswork'. It seems that :
\begin{align}
f(0)&=-\eta(0)-\frac i{\pi}\\
f\left(-\frac 12\right)&=-\eta\left(-\frac 12\right)+\frac 1{2\sqrt{2}\,\pi}(1-i)\\
f\left(\frac 12\right)&=-\eta\left(\frac 12\right)-\frac 1{\sqrt{2}}(1+i)\\
f\left(\frac 32\right)&=-\eta\left(\frac 32\right)+\sqrt{2}\,\pi(1-i)\\
\end{align}
Clearly we are not obtaining $f(s)=-\eta(s)$ but rather something like $$f(s)=-\eta(s)-\frac{(\pi\,i)^s}{\Gamma(s)}(1+i\cot(\pi\,s))$$
that may be simplified using the Euler reflection formula for $\Gamma$ : $\displaystyle \frac{\pi}{\sin(\pi s)\Gamma(s)}=\Gamma(1-s)$ and $\,e^{\pi\,is}=(-1)^s\,$ as :
$$\tag{3}f(s)=-\eta(s)-\Gamma(1-s)(-\pi\,i)^{s-1}$$
(numerically accurate for all the real and complex values of $s$ not integer tested!)
$$-$$
ADDITION (to thank Andrew!) Some pictures to 'show' what is happening.
The imaginary part of the zeta sum (formula $(2)$) for $s=x+iy$ is represented first.
Then the imaginary part of $-\eta(s)$ (formula $(1)$) at the same scale, the imaginary part changes in fact smoothly between $-0.45$ and $0.22$. The regularity of $\eta(s)$ in the complex domain shown is explained by the 'absorption' of the only singular part of $\zeta(s)$ (i.e. the pole at $s=1$) by $\left(2^{1-s}-1\right)$ to give $-\log(2)$.
Now the zeta sum $(2)$ contains not only the singularity of $\zeta$ at $s=1$ but also the transformed singularities at $s=2,\;3,\cdots$. The two last pictures show the sum $(2)$ but with only $2$ and $3$ terms respectively. The visual aspect of the poles is different because they 'rotate' with an angle $\dfrac{\pi}4$ and are vertically stretched.
Thus the point of the $\Gamma(1-s)(-\pi\,i)^{s-1}$ term in $3$ is to cancel all these poles at once ($\Gamma$ has poles at all the non positive integers) !
Let's start this again with a direct generalization involving the polylogarithm $\operatorname{Li}$ :
$$\operatorname{Li}_s(e^z):=\sum_{n=1}^\infty \frac {e^{nz}}{n^s}\quad\text{for}\; |e^z|<1$$
Using your method (with $\pi i$ replaced by $z$) we should obtain :
$$f_z(s):=\sum\limits_{k=0}^{\infty}\frac{z^k}{k!}\zeta(s-k)\overset{?}=\operatorname{Li}_s(e^z)$$
but get instead for $s$ not integer and $|z|<2\pi$ (or $\Re(z)\le 0$ only using the infinite sum for $\operatorname{Li}$) :
$$\sum\limits_{k=0}^{\infty}\frac{z^k}{k!}\zeta(s-k)=\operatorname{Li}_s(e^z)-\Gamma(1-s)(-z)^{s-1}$$
This result is given in Wikipedia's polylogarithm entry.
It appears too (with much more informations) in the chapter $5$ of an excellent article from Richard Crandall ($2012$) 'Unified algorithms for polylogarithm, L-series, and zeta variants'.
The part $2$ about the "periodic zeta function" from the $1976$ paper "On the evaluation of Euler sums" should be of interest too (consider $x=\dfrac 12$ and see $(2.7)$ to $(2.9)$ for your Bernoulli expansion).
The expression displayed is in fact the "Erdelyi expansion" for the polylogarithm which may be found in Srivastava and Choi's book "Series Associated With the Zeta and Related Functions".
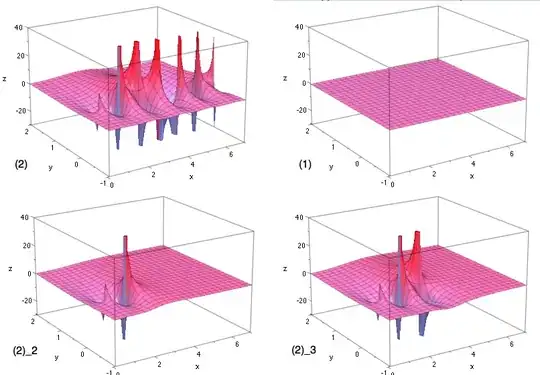
I reproduce here the pages $28-29$ from Erdelyi's ($1953$) "Higher transcendental functions $1$" (where a more general formula $(8)$ is obtained and the case $s$ integer is handled too in $(9)$).
Let's just start with the definitions of the Hurwitz zeta function and the Lerch transcendent :
\begin{align}
\zeta(s,v)&=\sum_{n=0}^\infty \frac 1{(v+n)^s}\\
\tag{1}\Phi(z,s,v)&=\sum_{n=0}^\infty \frac {z^n}{(v+n)^s}\\
\end{align}
$\qquad\qquad\Phi$ can be represented as a contour integral


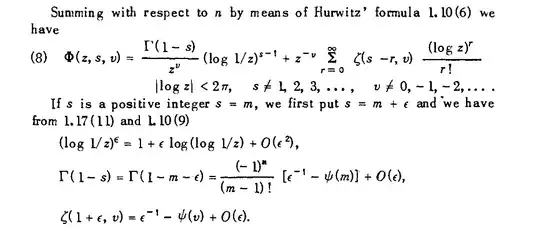
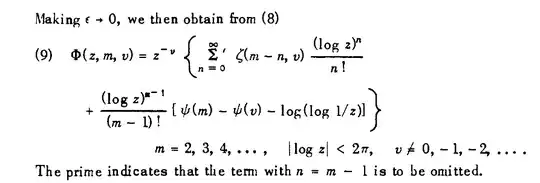
Where the Hurwitz formula $(1.10.6)$ is :
$$\zeta(s,v)=2(2\pi)^{s-1}\Gamma(1-s)\sum_{n=1}^\infty n^{s-1}\sin(2\pi n v+\pi s/2),\quad\Re(s)<0,\;0<v\le 1$$