What is this shape called?
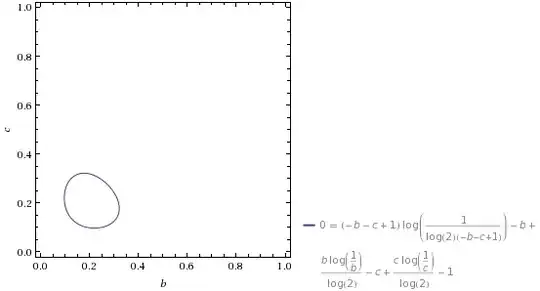
This would not fit in the comments
I think you may have made an error in your legend: by symmetry it is more likely to be something like $$(1-b-c)\log\left(\frac{1}{1-b-c}\right)/\log(2) + b\log\left(\frac{1}{b}\right)/\log(2) + c\log\left(\frac{1}{c}\right)/\log(2) - b - c - 1 = 0.$$
If so, this would be easier to read as $$(1-b-c)^{1-b-c} b^b c^c 2^{b+c+1} = 1$$ though that seems to have the real solution $b=c=1/4$ rather than your curve, so perhaps it should be something different.
Perhaps you could tell us the origin of your curve and the expression