The problem is, we do not know exactly what you mean by "idealised bean". Can you describe the shape better? A closed curve shape with two opposite indentations? (To me that seems more like a peanut.)
Then you say in the comments that $r = \sin^3\theta + \cos^3\theta$ seems to work well.
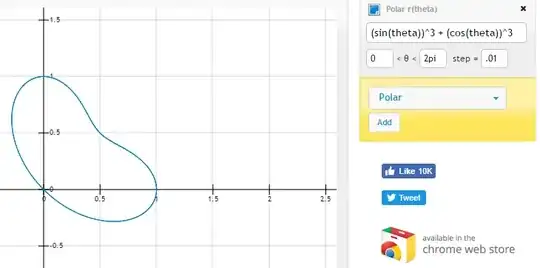
What do you want to do with that curve now? Give it another indentation on the opposite side?
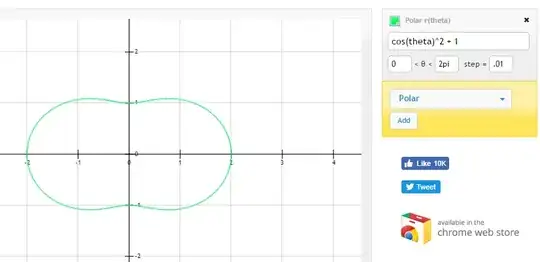
$r = \cos^2(\theta) + 1$
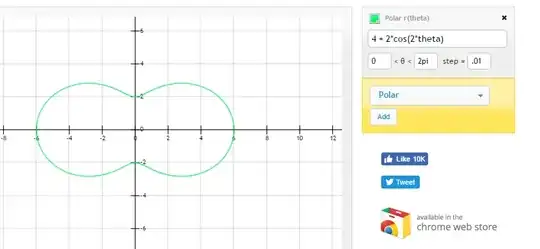
More indented with $r = 2\cos 2\theta + 4$
You also said "an ellipse/ellipsoid on a curved major axis." I'm not sure exactly what that looks like. If you can sketch the picture and show us, we'd have a better idea of the shape you're looking for.
BTW, to make 3D versions, usually we just rotate the 2D shape about some axis.
For reference, here are the equations for an ellipse:
$y = \pm b\sqrt{1 - \frac{x^2}{a^2}} \hspace{1cm}$ or $\hspace{1cm}r = \displaystyle \frac{ab}{\sqrt{a^2\sin^2\theta + b^2\cos^2\theta}}$ in polar coordinates.
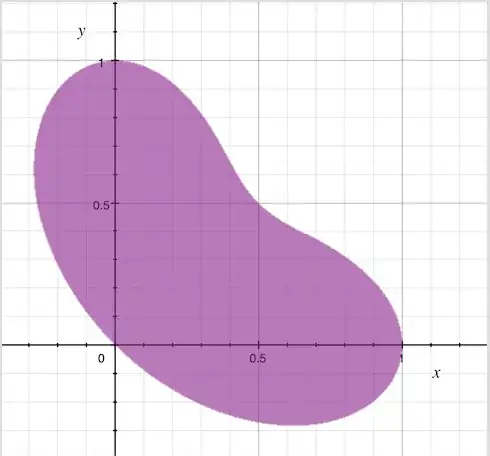



Edit: Oh, we're not actually naming this thing. Oops. Well it's homeomorphic to the unit ball, should we describe via homeomorphism?
– Gyu Eun Lee Dec 12 '12 at 07:50$\quad r=\sin^3\theta+\cos^3\theta$ – Elements In Space Dec 12 '12 at 08:05