The continuously differentiable functions are equipped with the topology induced by the sup norm. I know that I can make the arclength integral close to the arclength of a piecewise linear function. My idea is to take two functions which are adequately close together, and take two piecewise linear functions which are close to the integrals and show that we can make the difference of the arclength integral of the piecewise linear functions as small as we would like.
-
probably Fatou's Lemma ... – GEdgar Oct 06 '11 at 16:29
2 Answers
I don't think this is true:
For example $f: (0,1] \to \mathbb R$, $f(x) =c\sin\left(x^{-1}\right)$ has distance $c$ from $0$, but by considering it as a function on $[\delta, 1]$ for smaller and smaller delta, we can increase its length as much as we wish. (You can always reparametrize the so obtained function without changing the length, so for each $\delta >0$ we can get a function on $[0,1]$ which is $c$-close to $0$ and has arbitrarily big length)
Quite generally, the distance between two functions usually tells us almost nothing about the relationship of their derivatives (we always can find a function that oscillates wildly and has the same distance).
- 15,908
-
You're absolutely right Sam! It's lower semicontinuous. Do you know how to justify it being lower semicontinuous? – user11314 Oct 07 '11 at 03:08
This example was mentioned in a related question. I am adding it to this answer as well, just for the sake of completeness.
It is from the book Mathematical analysis: linear and metric structures and continuity by Mariano Giaquinta, Giuseppe Modica, p.204.
I hope it qualifies as fair use if I copy their picture.
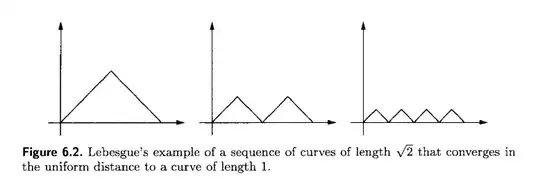
This example shows that length is not upper semicontinuous.
- 53,687
-
This example is basically same as this one: Is value of $\pi$ = 4 ? – Martin Sleziak Nov 13 '11 at 15:39