The Riemann Hypothesis is equivalent to the statement: $$|\pi(x)-{\rm li}(x)|\le \frac {1}{8\pi}\sqrt {x}\log (x)\text { for all }x \geq 2657,\text{ (Schoenfeld, 1976)}
$$
Which can be visually represented in the plot:
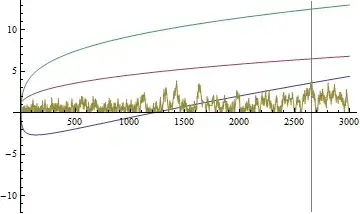 $$\text{with }\frac{1}{8\pi}\sqrt{x}\log(x)-|\text{J}(x)-\text{li}(x)|,\text{ (blue) }\\
\frac{\sqrt{x}}{\log(x)},\text{ (red) }\\
|\pi(x)-\text{J}(x)|,\text{ (yellow) }\\
|\text{J}(x)-\text{li}(x)|,\text{ (green) }\\
\text{where J}(x)=\sum_{n=1}^\infty\frac{\mu(n)}{n}\text{li}(x^{1/n});
$$
and on a larger scale:
$$\text{with }\frac{1}{8\pi}\sqrt{x}\log(x)-|\text{J}(x)-\text{li}(x)|,\text{ (blue) }\\
\frac{\sqrt{x}}{\log(x)},\text{ (red) }\\
|\pi(x)-\text{J}(x)|,\text{ (yellow) }\\
|\text{J}(x)-\text{li}(x)|,\text{ (green) }\\
\text{where J}(x)=\sum_{n=1}^\infty\frac{\mu(n)}{n}\text{li}(x^{1/n});
$$
and on a larger scale:
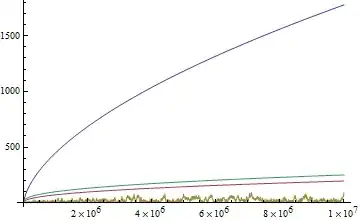
where it is not so difficult to imagine the oscillations crossing the green line eventually (Littlewood, 1914), but requires a leap of faith to say the least, that the oscillations will eventually cross the blue line. I believe I am correct in assuming that it is only the oscillations that are in question here, & not the general asymptotic of $J(x)$, but am willing to be corrected!
If the crossing of the oscillations of the green line begin at Skewe's number (whatever the actual value of that is), then if the RH is false, the magnitude of the number at which the oscillations cross the blue line must be significantly larger than that - which, even at the current rate of advances in computing, quantum computers being developed at some point in the future notwithstanding, I find it difficult to believe that the RH will be proven false in my lifetime (I am 37! - not factorial btw).
My question is, is the falsity of the RH (a) believable; and (b) ever provable (if, in the unlikely event that it is true) in terms of computing limits?
It seems to me, in the spirit of Hardy, to be an analogue of Russell's teapot analogy!