The Riemann Hypothesis is true if and only if Robin's Inequality is true for all n>5040. It has also been shown by Akbary and Friggstad that the smallest counterexample greater than 5040, if it exists, must be a Superabundant Number.
These two facts suggest that Robin's Inequality might provide a more elementary way to show the Riemann Hypothesis is true or help provide a counterexample in the form of a Superabundant Number which violates the inequality. Robin's Inequality is elegantly stated:
$$f(n)=\frac{\sigma (n)}{e^{\gamma} n \log \log n}<1$$
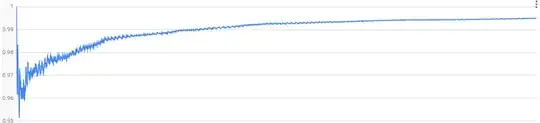
Below is a plot of the LHS for the first 2000 Superabundant Numbers above 5040 from A004394.
Looking at this plot and knowing how close the values get to 1 make it seem plausible that RH could be false, but if true it appears to be an asymptotically an increasing function bounded above by 1. Examining the remaining terms provided, the function behavior looks similar and for the largest term listed $f(a[1000000])\approx0.9998655$. No terms before the millionth cross the threshold of one and $a[1000000]\approx10^{103082}$.
Is this the highest known verification of RH? It is my understanding that ZetaGrid and others working with the zeta function directly have only verified zeros up to $10^{13}$. Also, from my understanding of Briggs he appears to have only verified completely up to $10^{154}$ using SA numbers?
In fact, based on this curve and the possible relationship shown here, I am willing to venture a conjecture.