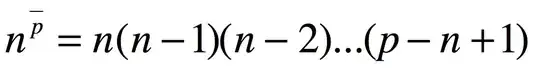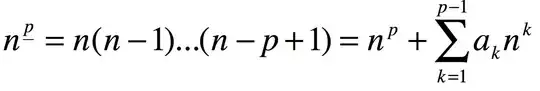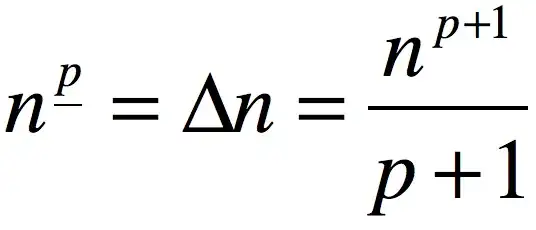Rising/Falling Powers, Summation

Question

1) Show that $$(-n)^{\bar p} = (-1)^n n^\underline{p}$$

(original screenshot)

2) Evaluate the sum $$\sum_{a\le n\lt b}n^{\bar p}$$

(original screenshot)

Thoughts regarding question 1:

I've presented some of my work below, however I am not certain how it applies to the questions presented above. For instance, in question one would you simply distribute the negative sign in front of n through the factored polynomial below? -1 to the nth power is either -1 or 1 depending on the value of n, so can that just be treated as a constant. In the case of question 1, it seems we are basically just manipulating the two factored polynomials.

Thoughts regarding question 2:

Here I believe some of my trouble lies with the bounds of the sum. It helps to think of the sum as n going from a to b-1. I'm pretty much stuck here. I know that in the question n is raised to the rising p-power, but in taking into account how you can write n to the falling p-power as a n raised to the p plus a sum, should it be the case that here the sum itself contain another sum?

Answer 1

Let's begin by considering the case where $p$ is even:

\begin{align} n^{\underline{p}}&=n(n-1)(n-2)\cdots(n-p+1) && \text{Definition of falling powers}\\ &=(-n)(-n+1)(-n+2)\cdots(-n+p-1) && \text{Multiply each term by } -1\\ &=(-n)^{\overline{p}} && \text{Definition of rising powers} \end{align}

In the case where $p$ is odd, multiplying each term by $-1$ changes the sign of the product, therefore $n^{\underline{p}}=-(-n)^{\overline{p}}$. In general

$$ n^{\underline{p}}=(-1)^p(-n)^{\overline{p}} $$

Equivalently, substituting $m=-n$ and rearranging gives

$$ m^{\overline{p}}=(-1)^p(-m)^{\underline{p}} $$

Let's now find the partial sum:

\begin{align} \sum\limits_{n=a}^{b-1} n^{\overline{p}} &= \sum\limits_{n=a}^{b-1}(-1)^p(-n)^{\underline{p}} \\ &=\sum\limits_{n=a}^{b-1}\Delta\left[-\frac{(-1)^p}{p+1}(-n)^{\underline{p+1}}\right]\\ &=\left.\frac{(-1)^{p+1}}{p+1}(-n)^{\underline{p+1}}\right|_{n=a}^b \\ &= \frac{(-1)^{p+1}}{p+1}\left[(-b)^{\underline{p+1}}-(-a)^{\underline{p+1}}\right] \\ &= \frac{(-1)^{p+1}}{p+1}\left[(-1)^{p+1}b^{\overline{p+1}}-(-1)^{p+1}a^{\overline{p+1}}\right] \\ &= \frac{b^{\overline{p+1}}-a^{\overline{p+1}}}{p+1} \\ \end{align}

where I used the discrete version of the Fundamental Theorem of Integral Calculus, the discrete derivative, and $(\Delta a)_n=a_{n+1}-a_n$ is the forward difference. These results are derived in an answer to another question about discrete calculus.