14

Doodling in wolfram, I found that $$ \sum^{k}_{n=1}1=k $$ The formula is pretty obvious, but then you get $$ \sum^{k}_{n=1}n=\frac{k(k+1)}{2} $$ That is a very well known formula, but then it gets interesting when you calculate $$ \sum^{k}_{n=1}n(n+1)=\frac{k(k+1)(k+2)}{3}\\ \sum^{k}_{n=1}n(n+1)(n+2)=\frac{k(k+1)(k+2)(k+3)}{4} $$ And so on. There is an obvious pattern that I really doubt is a coincidence, but I have no idea how to prove it in the general case. Any ideas?

MJD
  • 65,394
  • 39
  • 298
  • 580
chubakueno
  • 5,623
  • 1
    Pascal's triangle comes to mind here – Ben Grossmann Sep 04 '13 at 03:47
  • @Omnomnomnom I thought about it but I was unable to introduce binomials there. However, you can generalize the hypothesis using factorials, but usually working with factorials is harder than not doing so(At least I would have a very hard time trying to do so). – chubakueno Sep 04 '13 at 03:51
  • These are essentially the sums for the general $d$ dimensional simplex. – Jaycob Coleman Sep 04 '13 at 04:02
  • 2
    It's overkill, but you could expand and apply http://en.wikipedia.org/wiki/Faulhaber%27s_formula – dls Sep 04 '13 at 04:11
  • 1
    @dls I think that in that case the interesting part would go backwards: That expanding and a applying Faulhaber´s yields such a regular and simple result :) – chubakueno Sep 04 '13 at 04:22
  • There must be a simple proof of this that starts from the fact that $\nabla(x^{\overline m}) = mx^{\overline{m-1}},$ where $x^{\overline m}$ means $\frac{\Gamma(x+m)}{\Gamma(x)}$, and $\nabla$ is the backward difference operator $\nabla(f(x)) = f(x) - f(x-1)$; see Graham et al. Concrete Mathematics p. 49–49 and exercise 2.7 on p. 63. – MJD Sep 04 '13 at 06:15
  • You can probably get this just by staring at Pascal's triangle long enough. (You might want to divide your identity by $m!$ in each case, though, where $m$ is the number of factors in the thing you're summing.) – Akiva Weinberger Aug 09 '15 at 15:13

5 Answers5

7

Partial sums of sequences $a_n$ that can be expressed as polynomials in $n$ are easily found using discrete calculus.

We start with the discrete version of the Fundamental Theorem of Integral Calculus:

\begin{align*} \sum\limits_{n=1}^k a_n &= \sum\limits_{n=1}^k (\Delta b)_n \\ &= (b_2 - b_1)+(b_3 - b_2)+ \ldots + (b_k - b_{k-1}) + (b_{k+1} - b_k) \\ &= b_{k+1} - b_1 \end{align*}

where $(\Delta b)_n = b_{n+1} - b_n$ is the forward difference. Finding the partial sum has now been reduced to finding a sequence $b_n$ such that $(\Delta b)_n = a_n$.

We will find $b$, the antiderivative of $a$, using falling powers, which are defined by

$$ n^{\underline{k}} = n(n-1)(n-2)\ldots (n-k+1) $$

where $k$ is an integer and, by a second definition, $n^{\underline{0}}=1$. For example

$$ n^{\underline{3}} = n(n-1)(n-2). $$

We now need one more result: the discrete derivative of $n^{\underline{k}}$ is given by

\begin{align*} \Delta n^{\underline{k}} &= (n+1)^{\underline{k}} - n^{\underline{k}} \\ &= (n+1)n^{\underline{k-1}} - n^{\underline{k-1}}(n-k+1) \\ &= kn^{\underline{k-1}} \end{align*}

Let's now find the partial sum for a particular case:

\begin{align} \sum^{k}_{n=1}n(n+1)(n+2) &= \sum^{k}_{n=1} (n+2)^{\underline{3}} \\ &= \sum^{k}_{n=1} \Delta \left[\frac{1}{4} (n+2)^{\underline{4}}\right] \\ &= \frac{(k+3)(k+2)(k+1)k}{4} - \require{cancel}\cancelto{0}{\frac{(1+2)(1+1)(1-0)(1-1)}{4}} \end{align}

The general case:

\begin{align} \sum^{k}_{n=1} (n+p)^{\underline{p+1}} &= \sum^{k}_{n=1} \Delta \left[\frac{1}{p+2} (n+p)^{\underline{p+2}}\right] \\ &= \frac{(k+1+p)(k+p)\ldots [(k+1+p)-(p+2)+1)]}{p+2} \\ &= \frac{(k+1+p)(k+p)\ldots k}{p+2} \end{align}

where $p>0$ is an integer.

kwgoodman
  • 236
4

The easy way to deal, for example, with $\sum_{i=1}^n i(i+1)(i+2)(i+3)$ is to let $F(i)=i(i+1)(i+2)(i+3)(i+4)$. We calculate $F(i)-F(i-1)$. We get $$i(i+1)(i+2)(i+3)(i+4)-(i-1)(i)(i+1)(i+2)(i+3).$$ There is a common factor of $i(i+1)(i+2)(i+3)$. When we "take it out" we are left with $(i+4)-(i-1)=5$.

Let $G(i)=\frac{F(i)}{5}$. Then by our calculation $i(i+1)(i+2)(i+3)=G(i)-G(i-1)$.

Now consider the sum $\sum_{i=1}^n i(i+1)(i+2)(i+3)$. This is $$(G(1)-G(0))+(G(2)-G(1))+G(3)-G(2)) +\cdots+(G(n)-G(n-1)).$$ Observe the telescoping. Since $G(0)=0$, the above sum is equal to $G(n)$. Thus $$\sum_{i=1}^n i(i+1)(i+2)(i+3)=G(n)=\frac{n(n+1)(n+2)(n+3)(n+4)}{5}.$$

Exactly the same idea works in general.

André Nicolas
  • 507,029
2

The hypothesized equality can be written as follows: for any $m$, we conjecture $$ \sum^{k}_{n=1}\frac{(n+m)!}{(n-1)!}=\frac{(k+m+1)!}{(m+2)(k-1)!} $$ Dividing both sides by $(m+1)!$, we have $$ \sum^{k}_{n=1}\frac{(n+m)!}{(n-1)!(m+1)!}=\frac{(k+m+1)!}{(m+2)!(k-1)!} $$ Or, in other words $$ \sum^{k}_{n=1}\binom{n+m}{m+1}=\binom{k+m+1}{m+2} $$ I'm not sure how to prove this (yet), but it seems very likely that there's a neat trick for all this.

Ben Grossmann
  • 225,327
1

You can argue any given case by induction. I will take your last,$$\sum^{k}_{n=1}n(n+1)(n+2)=\frac{k(k+1)(k+2)(k+3)}{4}$$ for the example, but I think it is easy to see how it gets carried forward. The base case is simply $1\cdot 2\cdot 3=1\cdot 2\cdot 3\cdot \frac 44$ If it is true up to $k$, then $$\sum^{k+1}_{n=1}n(n+1)(n+2)\\=\sum^{k}_{n=1}n(n+1)(n+2)+(k+1)(k+2)(k+3)\\=\frac{k(k+1)(k+2)(k+3)}{4}+(k+1)(k+2)(k+3)\frac {k+4-k}4\\=\frac{(k+1)(k+2)(k+3)(k+4)}{4}$$

Ross Millikan
  • 374,822
  • Thanks! Just changing the $2$, $3$ and $4$ by $x$,$x+1$ and $x+2$ does the work of generalizing it very nicely. – chubakueno Sep 04 '13 at 03:59
0

[I haven't finished yet. Will be gradually improved]

If we do it this way, then probably, it will become more insightful.

$$ \sum^{k}_{n=1}1=k $$

then we preserve everything from the right side exactly as it is. $$ \sum^{k}_{n=1}n=\frac{k(k+1)}{1 \cdot 2} $$

The following picture explains this sum:

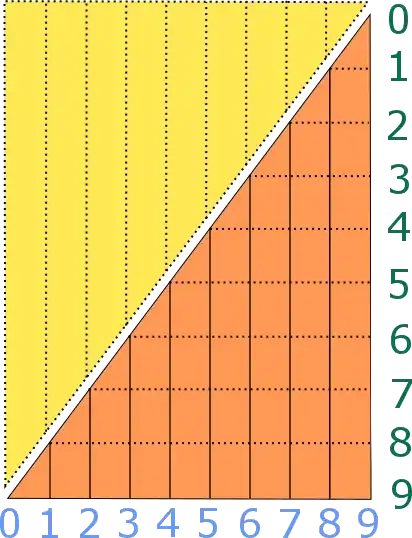
triange area

Now again, preserve everything from the right side: $$ \sum^{k}_{n=1}\frac{n(n+1)}{1 \cdot 2}=\frac{k(k+1)(k+2)}{1 \cdot 2 \cdot 3} $$

[there will be a picture of the 6 pyramids composed into rectangular parallelepiped]

$$ \sum^{k}_{n=1}\frac{k(k+1)(k+2)}{1 \cdot 2 \cdot 3}=\frac{k(k+1)(k+2)(k + 3)}{1 \cdot 2 \cdot 3 \cdot 4} $$

[There should be a description of the connection between simple combinations and combinations with repetition]

$$ {n \choose k} = \frac{n \cdot (n - 1) \cdot \ldots \cdot (n - k + 1)}{k \cdot (k - 1) \cdot \ldots \cdot 1} = \frac{n^{\underline{k}}}{k!} $$ $$ \left(\!\middle(\genfrac{}{}{0pt}{}{n}{k}\middle)\!\right) = \frac{n \cdot (n + 1) \cdot \ldots \cdot (n + k - 1)}{k \cdot (k - 1) \cdot \ldots \cdot 1} = \frac{n^{\overline{k}}}{k!} $$

Egor Okhterov
  • 409