How find this $$\prod_{n=2}^{\infty}\left(1-\dfrac{1}{n^6}\right)$$
I think we can find this value have closed form $$\prod_{n=2}^{\infty}\left(1-\dfrac{1}{n^{2k}}\right)$$ since $$1-\dfrac{1}{n^6}=\left(1-\dfrac{1}{n^3}\right)\left(1+\dfrac{1}{n^3}\right)$$ so I think we must find this $$\prod_{n=2}^{\infty}\left(1-\dfrac{1}{n^3}\right)$$ and $$\prod_{n=2}^{\infty}\left(1+\dfrac{1}{n^3}\right)$$
Thank you
As Mhenni Benghorbal mentioned, there is a similar problem which has been treated yesterday and I shall use a similar approach to the one he proposed.
$$\prod_{n=2}^{m}\left(1-\dfrac{1}{n^3}\right)=\frac{\cosh \left(\frac{\sqrt{3} \pi }{2}\right) \Gamma \left(m-\frac{i \sqrt{3}}{2}+\frac{3}{2}\right) \Gamma \left(m+\frac{i \sqrt{3}}{2}+\frac{3}{2}\right)}{3 \pi m^3 \Gamma (m)^2}$$ and $$\prod_{n=2}^{m}\left(1+\dfrac{1}{n^3}\right)=\frac{(m+1) \cosh \left(\frac{\sqrt{3} \pi }{2}\right) \Gamma \left(m-\frac{i \sqrt{3}}{2}+\frac{1}{2}\right) \Gamma \left(m+\frac{i \sqrt{3}}{2}+\frac{1}{2}\right)}{2 \pi \Gamma (m+1)^2}$$ So, the product, from $n=2$ to $n=m$, write $$\frac{(m+1) \cosh ^2\left(\frac{\sqrt{3} \pi }{2}\right) \Gamma \left(m-\frac{i \sqrt{3}}{2}+\frac{1}{2}\right) \Gamma \left(m-\frac{i \sqrt{3}}{2}+\frac{3}{2}\right) \Gamma \left(m+\frac{i \sqrt{3}}{2}+\frac{1}{2}\right) \Gamma \left(m+\frac{i \sqrt{3}}{2}+\frac{3}{2}\right)}{6 \pi ^2 m^5 \Gamma (m)^4}$$ If $m$ goes to infinity, the limit is then $$\frac{1+\cosh \left(\sqrt{3} \pi \right)}{12 \pi ^2} =\dfrac{\cosh^2\left(\pi\dfrac{\sqrt3}2\right)}{6\pi^2}$$ as shown by Lucian.
This is a method of directly evaluating the product which I have been applying to a number of products.
Set
\begin{align*} f(x) = x^3 \prod_{n=1}^\infty \left( 1 - \frac{x^6}{n^6} \right) \end{align*}
Taking logs and differentiating with respect to $x$ gives:
\begin{align*} \frac{d}{dx} \ln f(x) = \frac{3}{x} + \sum_{n=1}^\infty \dfrac{\left( - \frac{6x^5}{n^6} \right)}{\left( 1 - \frac{x^6}{n^6} \right)} = \frac{3}{x} -6 x^5 \sum_{n=1}^\infty \frac{1}{n^6 - x^6} \end{align*}
The sum can be evaluated by employing the fact that the function
\begin{align*} \dfrac{1}{\tan \pi z} \end{align*}
has simple poles at all integers $n$. This allows us to write
\begin{align*} \sum_{n=1}^\infty \frac{1}{n^6 - x^6} = \frac{1}{2 i} \oint_C \dfrac{1}{(z^6 - x^6) \tan \pi z} dz \end{align*}
where the contour $C$ is defined in fig (a). The dots are poles at non-zero integer values of $z$, whereas the crosses mark the location of the other poles of $\dfrac{1}{(z^6 - x^6) \tan \pi z}$.
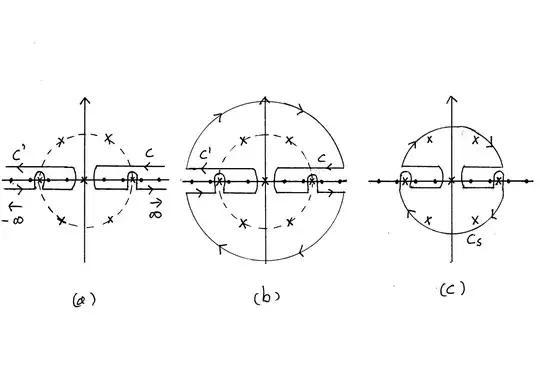
We have
\begin{align*} \sum_{n=1}^\infty \frac{1}{n^6 - x^6} & = \frac{1}{2} \sum_{n=1}^\infty \frac{1}{n^6 - x^6} + \frac{1}{2} \sum_{n=-1}^{-\infty} \frac{1}{n^6 - x^6} = \frac{1}{4 i} \oint_{C+C'} \dfrac{1}{(z^6 - x^6) \tan \pi z} dz \end{align*}
where the contour $C'$ is defined in fig (a). We complete the path of integration along semicircles at infinity (see fig (b)) since the integration along them vanishes. Since the resulting enclosed area contains a finite number of singularities marked by crosses, we can shrink this contour down to a contour, $C_s$, surrounding these finite number of poles (see fig (c)). So that
\begin{align*} \frac{d}{dx} \ln f(x) = \frac{3}{x} -6 x^5 \frac{1}{4i} \oint_{C_s} \frac{dz}{(z^6-x^6) \tan \pi z} \qquad (*) \end{align*}
The are poles at $z = 0, x, xe^{i2\pi/6}, xe^{i2\pi 2/6}, xe^{i2\pi 3/6} , xe^{i2\pi 4/6} , xe^{i2\pi 5/6}$. These are marked by crosses in the figures. Note
\begin{equation} \lim_{z \rightarrow x e^{ \frac{i 2 \pi q}{6} } } \frac{z^{6} - x^{6}}{z - x \frac{i 2 \pi q}{6}} = \lim_{z \rightarrow x e^{ \frac{i 2 \pi q}{6} } } \frac{\dfrac{d}{dz} (z^{6} - x^{6})}{\dfrac{d}{dz} (z - x \frac{i 2 \pi q}{6})} = \lim_{z \rightarrow x e^{ \frac{i 2 \pi q}{6} } } 6 z^5 = 6 x^5 e^{- \frac{i 2 \pi q}{6}} \end{equation}
Using this we evaluate $(*)$ to obtain
\begin{eqnarray} \frac{d}{dx} \ln f(x) & = \frac{3}{x} - 6 x^5 \frac{1}{4i} (-2 \pi i) \left[ \frac{1}{-x^6 \pi} + \sum_{q=0}^5 \dfrac{ e^{\frac{i 2 \pi q}{6}} }{6 x^5 \tan \pi (e^{\frac{i 2 \pi q}{6}} x)} \right] \nonumber \\ & = \frac{\pi}{2} \sum_{q=0}^5 \dfrac{ e^{\frac{i 2 \pi q}{6}} }{\tan \pi (e^{\frac{i 2 \pi q}{6}} x)} \end{eqnarray}
So that
\begin{eqnarray} \frac{d}{dx} \ln f(x) = \dfrac{1}{2} \left[ \sum_{q=0}^{5} \frac{d}{dx} \ln \sin [e^{\frac{i 2 \pi q}{6}} \pi x ] \right] \end{eqnarray}
and
\begin{eqnarray} f(x) = C \left[ \prod_{q=0}^5 \sin [e^{\frac{i 2 \pi q}{6}} \pi x ] \right]^{1/2} \end{eqnarray}
So
\begin{eqnarray} C \left[ \prod_{q=0}^5 \sin [e^{\frac{i 2 \pi q}{6}} \pi x ] \right]^{1/2} = x^3 \prod_{n=1}^\infty \left( 1 - \frac{x^6}{n^6} \right) \end{eqnarray}
Using $\lim_{x \rightarrow 0} \sin [A x]/x = A$, we have
\begin{equation} 1 = C \pi^3 \sqrt{ \prod_{q=0}^5 e^{ \frac{i 2 \pi q}{6} } } = C \pi^3 \sqrt{ e^{\frac{i 2 \pi [1+2+ \cdots + 5]}{6}} } = C \pi^3 \sqrt{ e^{ i \pi 5} } = C \pi^3 \sqrt{(-1)^{5}} = C \pi^3 i . \end{equation}
Therefore,
\begin{eqnarray} & x^3 \prod_{n=1}^\infty \left( 1 - \frac{x^6}{n^6} \right) = -i \frac{1}{\pi^3} \left[ \prod_{q=0}^5 \sin [e^{\frac{i 2 \pi q}{6}} \pi x ] \right]^{1/2} \nonumber \\ & = -i \frac{1}{\pi^3} \left[ (-\sin^2 (\pi x)) (- \sin^2 ([\frac{1}{2} + i \frac{\sqrt{3}}{2}] \pi x )) (- \sin^2 ([\frac{1}{2} - i \frac{\sqrt{3}}{2}] \pi x )) \right]^{1/2} \nonumber \\ & = \frac{1}{\pi^3} \sin (\pi x) \sin ([\frac{1}{2} + i \frac{\sqrt{3}}{2}] \pi x) ] \sin [\frac{1}{2} - i \frac{\sqrt{3}}{2}] \pi x) ]) \nonumber \\ & = \frac{1}{2\pi^3} \sin (\pi x) (\cosh (\sqrt{3} \pi x) - \cos (\pi x)) \end{eqnarray}
Therefore,
\begin{eqnarray} x^3 \prod_{n=1}^\infty \left( 1 - \frac{x^6}{n^6} \right) = \frac{1}{2 \pi^3} \sin (\pi x) (\cosh (\sqrt{3} \pi x) - \cos (\pi x)) \end{eqnarray}
Finally, dividing by $1 - x^6$ and taking the limit $x \rightarrow 1$ using l'Hopital
\begin{eqnarray} \prod_{n=2}^\infty \left( 1 - \frac{1}{n^6} \right) = \frac{1 + \cosh (\sqrt{3} \pi)}{12 \pi^2} \end{eqnarray}
$$P_6(x)=\prod_{n=1}^\infty\bigg(1-\frac{x^6}{\pi^6n^6}\bigg)=\frac{\sin x}{x^3}\cdot\frac{\cosh\big(x\sqrt3\big)-\cos x}2\quad$$
See Basel problem. For $x\to\pi$, use l'Hopital after first dividing through $1-\dfrac{x^6}{\pi^6}$ , in order to finally arrive at $\dfrac{\cosh^2\left(\pi\dfrac{\sqrt3}2\right)}{6\pi^2}$ . In general, $P_{2k}(x)=s_k\displaystyle\prod_{j=0}^{k-1}\frac{\sin\Big((-1)^{j/k}x\Big)}x$ , where $s_k$ forms a cycle of length four, $(+,+,-,-)$, starting with $k=1$. And, of course, when $x\to\pi$, use l'Hopital's rule after first dividing through $1-\bigg(\dfrac x\pi\bigg)^{2k}$, just as before. Hope this helps.
