9

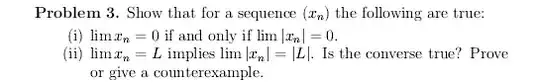
enter image description here

Problem 3. Show that for a sequence $(x_n)$ the following are true:
(i) $\lim x_n=0$ if and only if $\lim |x_n|=0$.
(ii) $\lim x_n=L$ implies $\lim |x_n|=|L|$. Is the converse true? Prove or give a counterexample.

(i) is already done, easy.

I'm halfway done with (ii), I split it into three cases:

$L = 0$, $L > 0$ and $L < 0$.

For $L = 0$ I just refer to part (i).

For $L > 0$, we know that $|x_n - L| < \epsilon$

if lim $|x_n|$ = $|L|$, then we must have

$||x_n| -|L|| < \epsilon$

but by the reverse triangle equality, $||x_n| - |L|| < |x_n - L|$ so clearly $||x_n|-|L|| < \epsilon$, thus

lim $x_n = L$ $\implies$ lim $|x_n| = |L|$ for $L > 0$

for some reason I'm confused as to part three, $L<0$. I'm having trouble seeing the difference between $L>0$ and $L<0$, and i'm starting to think that splitting it up like that isn't necessary at all.

Jonas Meyer
  • 53,602
terrible at math
  • 1,505

2 Answers2

14

For (ii) it's not necessary to split into $3$ cases: just write the definition using this inequality $$\left||x_n|-|L|\right|\le|x_n-L|$$ and for a counterexample take $$x_n=(-1)^n$$

2

You know $|x_n-L|<\varepsilon$ no matter the sign of $L$.

5xum
  • 123,496
  • 6
  • 128
  • 204