Derivatives of $\sinh x$ and $\cosh x$

Question

Can someone give me an intuitive explanation about the derivatives of $\sinh x$ and $\cosh x$? Something similar to:

Intuitive understanding of the derivatives of $\sin x$ and $\cos x$

Thanks!

Answer 1

There are the six hyperbolic functions and they are defined as follows.

Here are the graphs of the three main hyperbolic functions.

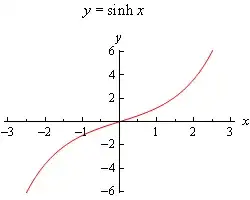
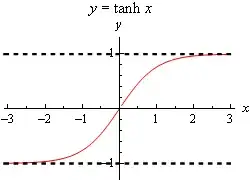
We also have the following facts about the hyperbolic functions.

You’ll note that these are similar, but not quite the same, to some of the more common trig identities so be careful to not confuse the identities here with those of the regular trig functions.

Because the hyperbolic functions are defined in terms of exponential functions finding their derivatives is fairly simple provided you’ve already knew. We haven’t however so we’ll need the following formula.

With this formula we’ll do the derivative for hyperbolic functions.

For the rest we can either use the definition of the hyperbolic function and/or the quotient rule. Here are all six derivatives.

Answer 2

In my opinion, the correct role of the trig functions in intuition is the other way around -- you shouldn't be trying to understand trig functions in terms of your intuition about other things: you should be trying to develop your intuition so that you understand other things in terms of trig functions.

(and, incidentally, this is in line with the general strategy that a good way to understand a mathematical idea, you need to understand how to use that idea to do things)

But anyways....

---

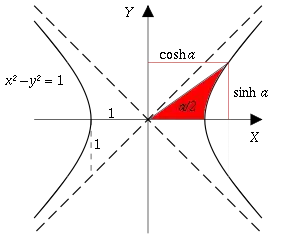
The unit circle is to the circular trig functions as the unit rectangular hyperbola is to the hyperbolic trig functions. The points $(\cosh u, \sinh u)$ trace out the points on the rightward-opening hyperbola defined by

$$ x^2 - y^2 = 1 \qquad \qquad x \geq 0 $$

The asymptote to this equation are the lines $y = \pm x$.

The parameter $u$ is the arclength from the point $(1,0)$ to the point $(\cosh u, \sinh u)$ along the hyperbola. Arclength is signed: so going "up" increases arclength, and "down" decreases arclength.

(note that the $\theta$ in $\cos \theta$ can be understood as arclength around the unit circle as well; the circle just has the nice fact that arclength and angle are the same)

If you studied hyperbolas as much as you studied circles, you would immediately know, for example, how to find the tangent line to a point on the hyperbola. But hyperbolas aren't studied so much these days, so it's unlikely that this has much utility.

---

There is a direct connection between the circular and hyperbolic functions in terms of the complex numbers: e.g.

• $\cos x = \cosh ix$
• $\sin x = -i \sinh ix$
• $\cosh x = \cos ix$
• $\sinh x = i \sin ix$

which, IMO, conveys intuition that any fact about the circular functions can be translated into an analogous fact about hyperbolic functions. e.g. I know that there is a double-angle formula for $\cos$. Therefore, there should be a similar double-angle formula for $\cosh$.

Answer 3

Intuitive not really, but why don't you look at the definition of for example $sinhx$? Take the derivative of the e-powers and due to the chain rule of the negative exponent ,it turns out you end up with $coshx$. Other than the fact that $sinhx$ is all increasing and derivative $coshx$ is always positive, there isn't much intuitive about it in my view.