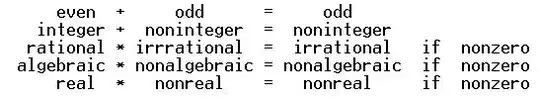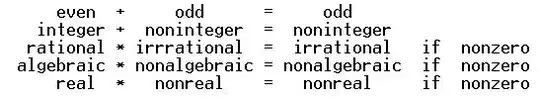The irrationals are the complement $\,\overline{\Bbb Q}\,$ of the subgroup $\Bbb Q\subset \Bbb C$. But a complement of subgroup is not a subgroup since it does not contain the identity $\,0,\,$ nor is it closed under subtraction, not containing $\,\alpha -\alpha.$ However, one can do some group-like calculations with such complements, such as: rational + irrational = irrational. Such statements are a special case of the following complementary view of a subgroup.
Theorem $\ $ Let $\rm\,G\,$ be a nonempty subset of an abelian group $\rm\,H,\,$ with complement set $\rm\,\bar G = H\backslash G.\,$
Then $\rm\,G\,$ is a subgroup of $\rm\,H\iff G + \bar G\, =\, \bar G. $
Proof $\ $ $\rm\,G\,$ is a subgroup of $\rm\,H\iff G\,$ is closed under subtraction, so, complementing
$\begin{eqnarray} & &\ \ \rm G\text{ is a subgroup of }\, H\ fails\\
&\iff&\ \rm\ G\ -\ G\ \subseteq\, G\,\ \ fails\\
&\iff&\ \rm\ g_1\, -\ g_2 =\,\ \bar g\ \ \ for\ some\ \ g_1,g_2\in G,\ \ \bar g\in \bar G\\
&\iff&\ \rm\ g_2\, +\ \bar g\ \ =\,\ g_1\ for\ some\ \ g_1,g_2\in G,\ \ \bar g\in \bar G\\
&\iff&\ \rm\ G\ +\ \bar G\ \subseteq\ \bar G\ \ fails\qquad\ {\bf QED}
\end{eqnarray}$
Instances of this are ubiquitous in concrete number systems, e.g. below. For many further examples see some of my prior posts here.