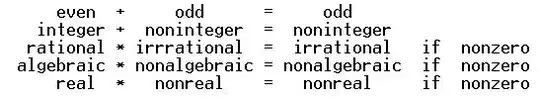Is the sum of a rational function and polynomial a rational function?

Question

Suppose $r(x)\neq 0$ is a rational function (and not a polynomial), and $p(x)$ is a polynomial function of $x \in \mathbb R$.

Does it follow that $r(x)+p(x)$ is a rational function (and not a polynomial)?

Answer 1

Yes. Suppose that $r(x)+p(x)=s(x)$ were a polynomial. Then also $r(x)=s(x)-p(x)$ would be a polynomial, hence $r(x)$ is a polynomial, contradiction.

Answer 2

Hint $\ $ Note that the set $\rm S\,$ of polynomials are closed under subtraction so they comprise an additive subrgoup of the additive group $\rm G$ of rational functions. Now apply the following

Theorem $ $ A nonempty subset $\rm\:S\:$ of abelian group $\rm\:G\:$ comprises a subgroup $\rm\iff\ S\ + \ \bar S\ =\ \bar S\ $ where $\rm\: \bar S\:$ is the complement of $\rm\:S\:$ in $\rm\:G$

Here is the simple proof. Instances of this "complementary view of a subgroup" are ubiquitous