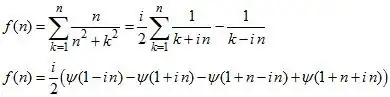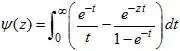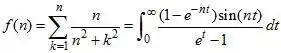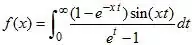How prove this $f(n)\le f(n+1)$ where $f(n)=\sum_{k=1}^{n}\frac{n}{n^2+k^2}$

Question

let $$f(n)=\sum_{k=1}^{n}\dfrac{n}{n^2+k^2}$$

prove or disprove $$f(n)\le f(n+1)$$

this inequality is found when I deal this follow limit: $$\lim_{n\to\infty}f(n)=\lim_{n\to\infty}\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{1}{1+(k/n)^2}=\int_{0}^{1}\dfrac{1}{1+x^2}dx=\dfrac{\pi}{4}$$ But I can't prove $$f(n)\le f(n+1)$$

since $$f(n+1)=\dfrac{n+1}{(n+1)^2+1}+\dfrac{n+1}{(n+1)^2+2^2}+\cdots+\dfrac{n+1}{(n+1)^2+n^2}+\dfrac{n+1}{(n+1)^2+(n+1)^2}$$ $$f(n)=\dfrac{n}{n^2+1}+\dfrac{n}{n^2+2^2}+\cdots+\dfrac{n}{n^2+n^2}$$ so $$f(n+1)-f(n)=\left(\dfrac{n+1}{(n+1)^2+1}-\dfrac{n}{n^2+1}\right)+\left(\dfrac{n+1}{(n+1)^2+2^2}-\dfrac{n}{n^2+2^2}\right)+\cdots+\left(\dfrac{n+1}{(n+1)^2+n^2}-\dfrac{n}{n^2+n^2}\right)+\dfrac{1}{2(n+1)}$$ so $$f(n+1)-f(n)=\sum_{k=1}^{n}\dfrac{k^2-n^2-n}{(k^2+n^2)((n+1)^2+k^2)}+\dfrac{1}{2(n+1)}$$

This problem is my found it,can you help to solve this problem?

Answer 1

Take $g(x):=\frac{1}{n^2+x^2}$ and apply the Euler-MacLaurin's summation formula. , Then we obtain $$ f(n)=\frac{\pi}{4}-\frac{1}{4n}+h(n),\qquad |h(n)|\leq\frac{3^{3/2}-2}{32n^2}. $$ From this $$ f(n+1)-f(n)=\frac{1}{4n(n+1)}+H(n),\qquad |H(n)|\leq\frac{3^{3/2}-2}{16n^2}. $$ It yields $$ f(n+1)-f(n)\geq\frac{(6-3^{3/2})n-3^{3/2}+2}{16n^2(n+1)}, $$ which is positive if $n\geq4$. For $n=1,2,3$ it can be checked by hand.

Answer 2

This answer is essentially the same approach as vesszabo's; I include it just to give another perspective. Set $g(x)=1/(1+x^2)$. Consider the trapezoidal approximation $$\int_0^1 g(x) dx \approx \frac{1}{n} \left( \frac{g(0)+g(1/n)}{2} + \frac{g(1/n)+g(2/n)}{n} + \cdots + \frac{g((n-1)/n)+ g(1)}{2} \right)$$ $$=\frac{1}{2n} + f(n) - \frac{1}{4n}.$$ It is well known that the error in the trapezoidal approximation is $-(1-0)^3 M/(12 n^2)$ where $M = g''(x)$ for some $x \in [0,1]$. NEXT PART IS UPDATED, thanks to zyx for pointing out the error. The most positive value of $g''$ is $1/2$, at $x=1$, and the most negative is $-2$ at $x=0$.

So $$ \int_0^1 g(x) dx - \left( \frac{1}{2n} + f(n) - \frac{1}{4n} \right) \geq - \frac{1}{24 n^2}$$ or, after a little algebra, $$f(n) \leq \frac{\pi}{4} - \frac{1}{4n} + \frac{1}{24 n^2}.$$

Similarly, $$f(n+1) \geq \frac{\pi}{4} - \frac{1}{4(n+1)} - \frac{1}{6(n+1)^2}$$

So $$f(n+1) - f(n) \geq \frac{n^2 + 4n -1}{24 n^2 (n+1)^2}$$ which is $>0$ for $n \geq 1$.

The basic point here is that, when comparing a sum to an integral, your first approach should be Riemann sums (tried by Did, but not good enough), your second should be the trapezoidal rule (used here), and the third should be the full power of Euler-Maclaurin summation (vesszabo's answer).

Answer 3

(Partial answer, more some remarks actually.)

These are Riemann sums $f(n)=\frac1n\sum\limits_{k=1}^ng\left(\frac{k}n\right)$ where $g:x\mapsto\frac1{1+x^2}$ on $[0,1]$.

• Since $g$ is decreasing and the Riemann sums are based on the right endpoints of the intervals $\left[\frac{k-1}n,\frac{k}n\right]$, one knows that $f(n)\lt\ell$ for every $n$, where $\ell=\lim\limits_{n\to\infty}f(n)=\int\limits_0^1g=\frac\pi4$.
• The intervals of the partition into $nk$ intervals are subintervals of those of the partition into $n$ intervals hence the same argument shows that $f(n)\lt f(nk)$ for every $n\geqslant1$ and $k\geqslant2$, for example $f(2^n)\lt f(2^{n+1})$ for every $n\geqslant0$.

A proof of the full monotonicity of $(f(n))$, if this property holds, might use more refined properties of $g$ than its monotonicity, perhaps its convexity/concavity properties on $[0,1]$.

Answer 4

This might lead to a solution, but at the very least, demonstrates just how delicate the estimate is.

We want to get a grip on $$ S_n = \sum_{k = 1}^n \frac{n^2 + n - k^2}{(n^2 + k^2) ((n+1)^2 + k^2)} $$ and show that it dies faster than $\frac{1}{2n}$. Let's be cavalier and drop the '$n+1$' business in the denominator, to make our lives simpler. Then, we're bounding $$ S_n' = \sum_{k = 1}^n \frac{n^2 + n - k^2}{(n^2 + k^2)^2} = \frac{1}{n^2} \left(\sum_{k = 1}^n \frac{1-(k/n)^2}{(1 + (k/n)^2)^2} + \frac{1}{n} \frac{1}{(1 + (k/n)^2)^2} \right) $$ We can realize this as a pair of Riemann sums: the first (dominant) term is the right-endpoint Riemann sum of the decreasing function $g_1(x) = \frac{1-x^2}{(1 + x^2)^2}$, and the second term is the right-endpoint Riemann sum of $g_2(x) = \frac{1}{(1+x^2)^2}$. Both of these Riemann sums will be strictly smaller than their destined integrals. Now the fun part: $$ \int_0^1 g_1(x) dx = \frac{1}{2} $$ and so for large $n$, the dominant term is just just barely small enough to conclude. To make this a proof, one would have to find a lower bound for the error in the Riemann sum of $g_1$ along $[0,1]$, and compare this with the $g_2$ term. Thankfully, $g_1$ is actually concave on $[0,\sqrt{2}-1]$, and so there is some hope of taking a small subinterval in there and cooking up a lower bound for this error that defeats the $g_2$ term.

---

I did out the following. It didn't work the way I hoped, but I figured I would record the method here, if someone can improve it.

WolframAlpha computes the integral $\int_0^1 g_2(x) dx = \frac{2 + \pi}{8} \leq \frac{7}{10}$ and $\int_{2/5}^1 g_1(x) dx = 9/58, \int_{0}^{1/5} g_1(x) dx = \frac{5}{26}$. So, $$ S_n \leq S_n' \leq \frac{1}{n^2} \sum_{k = \lfloor \frac{n}{10} \rfloor }^{ \lceil \frac{2 n}{5}\rceil } g_1(\frac{k}{n}) + \frac{C}{n} + \frac{7}{10 n^2} $$ with $C = \frac{9}{58} + \frac{5}{26}$. (the above might be off by a term or two in the remaining sum) We truncate the Riemann sum for $g_1$ from $2/5$ to $1$ because $g_1$ isn't concave there, and we truncate from $0$ to $1/5$ so that we have a positive lower bound on $g_1'$ on $[1/5, 2/5]$.

Now, $g_1'(x) \leq - 1$ for $x \in [1/5,2/5]$; each of the vertical strip segments in the remaining part of the Riemann sum will underestimate the true integral of $g_1$ there by at least $\frac{1}{n^2}$. In total, the underestimation contribution to the total Riemann sum from such terms is at least $\frac{n }{5} \cdot \frac{1}{ n^2} = \frac{1}{5 n}$, and so we have shown that $$ S_n' \leq \frac{1}{n}\left(\frac{1}{2} - \frac{1}{5 n} + \frac{7}{10 n}\right) $$

Unfortunately this isn't strong enough. I don't think adjusting the endpoints will work: one probably has to make a more careful estimate using additionally the (nonconcave) segment $[2/5,1]$.

Answer 5

This in fact is an extension of the question initially raised.

The finite series can be expressed in terms of digamma function :

Using the integral definition of the digamma :

The finite series can be expressed as a function defined by an integral:

Then the function with integer n is extended to the positive reals x :

The function $f(x)$ is continuous and can be graphically represented :

This shows that $f(x)$ is continuously increassing. As a consequence, we can extend the initial question $f(n+1)>f(n)$ to an extended one $f(x+r)>f(x)$ where $x$ and $r$ are any positive reals.

Of course, the graphical presentation is not an analytical proof.

Answer 6

The inequality is true for large $n$ based on general principles, but having it for all $n$ starting from $n=1$ is "accidental".

For any smooth function $g(x)$ on a closed finite interval, its Riemann sums $f(n)$ (for any of the usual choices of $n$ points and their weights) have an asymptotic expansion in powers of $1/n$. Therefore an expansion $(f(n+1)- f(n)) \sim \frac{A}{n} + \frac{B}{n^2} + \dots$ also exists and the sign of the first nonzero term will determine the direction of monotonicity, for large $n$. Euler-Maclaurin formula with remainder can be used to find $n_0$ such that the monotonicity holds for $n \geq n_0$, but monotonicity can fail for small $n$.

In this problem the direction of monotonicity is known without calculations, because $f(n)$ is the upper-endpoint Riemann sum of a decreasing function $g(x)$, so that $f(2n) \geq f(n)$ from one Riemann partition refining the other. We know this way that $f(n)$ is eventually increasing.

For a decreasing convex $g(x)$, with $g' \leq 0 \leq g''$ the $f(n)$ type of Riemann sums do monotonically increase for all $n \geq 1$. This is a frequently rediscovered theorem but it does not apply to $g(x)=\frac{1}{1+x^2}$ on $[0,1]$ because $g''(x)$ changes sign in that interval. Apparently there is nothing more that can be done except to compute the first terms in the Euler-Maclaurin formula, estimate the error term (which for this problem means determining a bound on $|g''|$) to compute an $n_0$, and check the inequality for smaller $n$ by computation. Which is exactly what is done in the other answers that reached a conclusion.

It is interesting that this problem was found by calculation with small $n$, because according to this analysis those are the $n$ that do not matter and can violate the general pattern that does hold for large $n$.

Answer 7

This is a comment that’s too long for the usual format. Let $g(x)=\dfrac{1}{1+x^2}$. Let us generalize the original question by putting for any $y \geq x \geq 0$,

$$ \begin{array}{lcl} u_n(x,y)&=&\frac{1}{n}\sum_{k=1}^{n} g\left(x+\frac{k}{n}(y-x)\right) \\ f_n(x,y)&=& u_{n+1}(x,y)-u_n(x,y) \\ \end{array} $$

Conjecture $f_n(x,y)$ can be written

$$ f_n(x,y)=(y-x)h_n(x,y)\prod_{k=1}^n g\left(x+\frac{k}{n}(y-x)\right)g\left(x+\frac{k}{n+1}(y-x)\right) $$

where $h_n$ is a polynomial with nonnegative coefficients in $x,y$.

I have checked this conjecture up to $n=10$, and it clearly is stronger than the original claim.