Show that: $$\left(\dfrac{n}{n+1}\right)^{n+1}<\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}<\left(\dfrac{n}{n+1}\right)^n$$ where $n\in \Bbb N^{+}.$ creat by( wang yong xi)
If this inequality can be proved, then we have $$\lim_{n\to\infty}\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}=\dfrac{1}{e}.$$
But I can't prove this inequality. Thank you.
Hint:
Applying Stolz–Cesàro theorem
$$L=\lim_{n\to \infty} \frac{\sqrt[n]{n!}}{n}=\lim_{n\to \infty} \frac{\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}}{(n+1)-n}=\lim_{n\to \infty} \left(\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\right)$$
We have $$\ln L=\lim_{n\to \infty} \left(\frac{1}{n}\sum_{i=0}^{n}\ln\left(\frac{i}{n}\right)\right)=\int_{0}^{1}\ln x\,dx=-1$$
$$\to L=\frac{1}{e}$$
Evaluating the Limit
Consider $$ \lim_{n\to\infty}\frac{\log(n!)-n\log(n)}{n}\tag{1} $$ Using Stolz-Cesàro, this is $$ \begin{align} &\lim_{n\to\infty}\frac{\big[\log((n+1)!)-(n+1)\log(n+1)\big]-\big[\log(n!)-n\log(n)\big]}{[n+1]-n}\\ &=\lim_{n\to\infty}n\log\left(\frac{n}{n+1}\right)\\[6pt] &=-1\tag{2} \end{align} $$ Therefore, $$ \lim_{n\to\infty}\frac{n!^{\frac1n}}{n}=\frac1e\tag{3} $$ Inverting $\lim\limits_{n\to\infty}\left(1+\frac xn\right)^n=e^x$, we have $$ \lim_{n\to\infty}n\left(x^{1/n}-1\right)=\log(x)\tag{4} $$ Using the equation $$ \begin{align} (n+1)!^{\frac1{n+1}}-n!^{\frac1n} &=\frac{n!^{\frac1n}}{n+1}(n+1)\left(\left(\frac{n+1}{n!^{\frac1n}}\right)^{\frac1{n+1}}-1\right)\tag{5} \end{align} $$ and $(3)$ and $(4)$, we get $$ \begin{align} \lim_{n\to\infty}(n+1)!^{\frac1{n+1}}-n!^{\frac1n} &=\lim_{n\to\infty}\frac{n!^{\frac1n}}{n+1}(n+1)\left(\left(\frac{n+1}{n!^{\frac1n}}\right)^{\frac1{n+1}}-1\right)\\ &=\lim_{n\to\infty}\frac1e(n+1)\left(e^\frac1{n+1}-1\right)\\[9pt] &=\frac1e\log(e)\\[9pt] &=\frac1e\tag{6} \end{align} $$ I'm still working on a simple derivation of the initial inequality, however.
Asymptotic Expansions
This is not what I would call simple, but it does show that, at least asymptotically, the initial inequality is true.
Using the Euler-Maclaurin Sum Formula, we get the formula $$ \log(n!)=\frac12\log(2\pi n)+n\log(n)-n+\frac1{12n}-\frac1{360n^3}+\frac1{1260n^5}+O\!\left(\frac1{n^7}\right)\tag7 $$ and therefore, $$ \frac1n\log(n!)=\log(n)-1+\frac12\frac{\log(2\pi n)}n+\frac1{12n^2}-\frac1{360n^4}+\frac1{1260n^6}+O\!\left(\frac1{n^8}\right)\tag8 $$ The constant $\frac12\log(2\pi)$ is gotten elsewhere (e.g. see this answer).
Using $\log(n+1)=\log(n)+\frac1n-\frac1{2n^2}+\frac1{3n^3}-\frac1{4n^4}+\dots$, we get $$ \log((n+1)!)=\frac12\log(2\pi n)+(n+1)\log(n)-n+\frac{13}{12n}-\frac1{2n^2}+O\!\left(\frac1{n^3}\right)\tag9 $$ and therefore, using $\frac1{n+1}=\frac1n-\frac1{n^2}+\frac1{n^3}-\frac1{n^4}+O\!\left(\frac1{n^5}\right)$, we get $$ \scriptsize\frac1{n+1}\log((n+1)!)=\log(n)-1+\frac12\frac{\log(2\pi n)}{n}+\frac1n-\frac12\frac{\log(2\pi n)}{n^2}+\frac1{12n^2}+O\!\left(\frac{\log(n)}{n^3}\right)\tag{10} $$ Exponentiating $(8)$ and $(10)$ and subtracting gives $$ \bbox[5px,border:2px solid #C0A000]{\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}=\frac1e\left(1+\frac1{2n}-\frac{5+3\log(2\pi n/e)^2}{24n^2}+O\!\left(\frac{\log(n)^3}{n^3}\right)\right)}\tag{11} $$ Using $\log\left(\frac{n}{n+1}\right)=-\frac1n+\frac1{2n^2}-\frac1{3n^3}+O\!\left(\frac1{n^4}\right)$ yields $$ \bbox[5px,border:2px solid #C0A000]{\left(\frac{n}{n+1}\right)^n=\frac1e\left(1+\frac1{2n}-\frac5{24n^2}+O\!\left(\frac1{n^3}\right)\right)}\tag{12} $$ and $$ \bbox[5px,border:2px solid #C0A000]{\left(\frac{n}{n+1}\right)^{n+1}=\frac1e\left(1-\frac1{2n}+\frac7{24n^2}+O\!\left(\frac1{n^3}\right)\right)}\tag{13} $$ Thus, asymptotically, $$ \left(\frac{n}{n+1}\right)^n-\left(\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\right)\sim\frac{\log(2\pi n/e)^2}{8n^2}\tag{14} $$ which is far smaller than $$ \left(\frac{n}{n+1}\right)^n-\left(\frac{n}{n+1}\right)^{n+1}\sim\frac1{en}\tag{15} $$
Graphical Comparisons
Graphically, we can see the size difference between $(14)$, the distance between the top two functions, and $(15)$, the distance between the top and bottom functions.
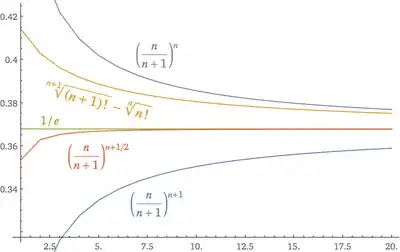
Remark: I proved the second inequality. Maybe the first inequality can be proved in similar way. I have not yet tried it. I used Maple software.
Let us prove that $$\sqrt[n+1]{(n+1)!} - \sqrt[n]{n!} < \Big(\frac{n}{n+1}\Big)^n, \quad \forall n\ge 1.$$
We first introduce some auxiliary results (Facts 1 through 6) used to prove the inequality.
Fact 1: For all integers $n\ge 1$, we have \begin{align} \sqrt[n]{n!} &> \sqrt[2n]{\pi}\, \frac{n}{\mathrm{e}} \sqrt[6n]{8n^3 + 4n^2 + n + \frac{1}{100}}, \\ \sqrt[n]{n!} &< \sqrt[2n]{\pi}\, \frac{n}{\mathrm{e}} \sqrt[6n]{8n^3 + 4n^2 + n + \frac{1}{30}}, \\ \sqrt[n+1]{(n+1)!} &< \sqrt[2n+2]{\pi}\, \frac{n+1}{\mathrm{e}} \sqrt[6n+6]{8n^3 + 28n^2 + 33n + \frac{391}{30}}. \end{align} See: G. E. Andrews and B. C. Berndt, Ramanujan's Lost Notebook Part IV, 2013, page 111.
Fact 2: For all integers $n\ge 1$, we have $$\ln \Big(8n^3 + 28n^2 + 33n + \frac{391}{30}\Big) - \ln \Big(8n^3 + 4n^2 + n + \frac{1}{100}\Big) < \frac{3}{n} - \frac{2}{n^2} + \frac{3607}{2400n^3}.$$ The proof is simple and thus omitted.
Fact 3: For all integers $n\ge 1$, we have $$\ln (8n^3 + 4n^2 + n + \frac{1}{100}) > 3\ln 2 + 3\ln n + \frac{1}{2n} - \frac{47}{2400n^3}.$$ The proof is simple and thus omitted.
Fact 4: For all integers $n\ge 1$, we have $$\ln (8n^3 + 4n^2 + n + \frac{1}{30}) < 3\ln 2 + 3\ln n + \frac{1}{2n}.$$ The proof is simple and thus omitted.
Fact 5: For all integers $n\ge 1$, we have $$n\ln n - n \ln (n+1) > -1 + \frac{1}{2n} - \frac{1}{3n^2}.$$ The proof is simple and thus omitted.
Fact 6: For all integers $n\ge 1$, we have $$\sqrt[n+1]{(n+1)!} < \Big(1 + \frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big)\sqrt[n]{n!}.$$ The proof is given later.
$\phantom{2}$
Now let us begin. If $1 \le n\le 5$, the inequality is verified directly. In the following, we assume that $n \ge 6$.
According to Fact 6, it suffices to prove that $$\Big(\frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big)\sqrt[n]{n!} < (\frac{n}{n+1})^n.$$ According to Fact 1, it suffices to prove that \begin{align} &\ln \Big(\frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big) + \frac{1}{2n}\ln \pi + \ln n - 1 + \frac{1}{6n}\ln (8n^3 + 4n^2 + n + \frac{1}{30})\\ <\ & n\ln n - n \ln (n+1). \end{align} According to Fact 4 and 5, it suffices to prove that \begin{align} &\ln \Big(\frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big) + \frac{1}{2n}\ln \pi + \ln n - 1 + \frac{1}{6n}(3\ln 2 + 3\ln n + \frac{1}{2n})\\ <\ & -1 + \frac{1}{2n} - \frac{1}{3n^2}. \end{align} Let \begin{align} G(x) &= -1 + \frac{1}{2x} - \frac{1}{3x^2} - \ln \Big(\frac{1}{x} - \frac{\ln x + \ln 2\pi - 1}{2x^2}\Big)\\ &\quad - \Big(\frac{1}{2x}\ln \pi + \ln x - 1 + \frac{1}{6x}(3\ln 2 + 3\ln x + \frac{1}{2x})\Big). \end{align} We have $$G'(x) = \frac{1}{6x^3(2x - \ln x - \ln 2\pi + 1)}(p_2(\ln x)^2 + p_1 \ln x + p_0)$$ where \begin{align} p_2 &= -3x, \\ p_1 &= -(6\ln 2\pi - 9)x - 5, \\ p_0 &= (-3\ln^2 2\pi + 9\ln 2\pi +4)x + 5 - 5\ln 2\pi. \end{align} Clearly, $p_2, p_1 < 0$ for $x \ge 1$. Since $\ln x > \frac{2(x-1)}{x+1}$ for $x > 1$, we have $$p_2(\ln x)^2 + p_1 \ln x + p_0 < p_2\Big(\frac{2(x-1)}{x+1}\Big)^2 + p_1\frac{2(x-1)}{x+1} + p_0, \quad \forall x \ge 6.$$ It is easy to prove that $$p_2\Big(\frac{2(x-1)}{x+1}\Big)^2 + p_1\frac{2(x-1)}{x+1} + p_0 < 0, \quad \forall x \ge 6.$$ Thus, $G'(x) < 0$ for $x\ge 6$. Note also that $\lim_{x\to \infty} G(x) = 0$. Thus, we have $G(x) > 0$ for $x\ge 6$. This completes the proof.
$\phantom{2}$
Proof of Fact 6: If $1 \le n\le 3$, the inequality is verified directly. In the following, we assume that $n \ge 4$. We need to prove that \begin{align} \ln \sqrt[n+1]{(n+1)!} < \ln \sqrt[n]{n!} + \ln \Big(1 + \frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big). \end{align} According to Fact 1, it suffices to prove that \begin{align} &\frac{1}{2n+2}\ln \pi + \ln (n+1) - 1 + \frac{1}{6n+6}\ln (8n^3 + 28n^2 + 33n + \frac{391}{30})\\ < \ & \frac{1}{2n}\ln \pi + \ln n - 1 + \frac{1}{6n}\ln (8n^3 + 4n^2 + n + \frac{1}{100})\\ &\quad + \ln \Big(1 + \frac{1}{n} - \frac{\ln n + \ln 2\pi - 1}{2n^2}\Big) \end{align} or \begin{align} & \frac{1}{6n+6}\Big(\ln (8n^3 + 28n^2 + 33n + \frac{391}{30}) - \ln (8n^3 + 4n^2 + n + \frac{1}{100})\Big)\\ < \ & \frac{1}{2n(n+1)}\ln \pi + \frac{1}{6n(n+1)}\ln (8n^3 + 4n^2 + n + \frac{1}{100})\\ &\quad + \ln \Big(1 - \frac{\ln n + \ln 2\pi - 1}{2n(n+1)}\Big). \end{align} According to Fact 2 and 3, it suffices to prove that \begin{align} & \frac{1}{6n+6}\Big(\frac{3}{n} - \frac{2}{n^2} + \frac{3607}{2400n^3}\Big)\\ < \ & \frac{1}{2n(n+1)}\ln \pi + \frac{1}{6n(n+1)} \Big(3\ln 2 + 3\ln n + \frac{1}{2n} - \frac{47}{2400n^3}\Big)\\ &\quad + \ln \Big(1 - \frac{\ln n + \ln 2\pi - 1}{2n(n+1)}\Big). \end{align} Let \begin{align} F(x) &= \frac{1}{2x(x+1)}\ln \pi + \frac{1}{6x(x+1)}\Big(3\ln 2 + 3\ln x + \frac{1}{2x} - \frac{47}{2400x^3}\Big)\\ &\quad + \ln \Big(1 - \frac{\ln x + \ln 2\pi - 1}{2x(x+1)}\Big) - \frac{1}{6x+6}\Big(\frac{3}{x} - \frac{2}{x^2} + \frac{3607}{2400x^3}\Big). \end{align} We have $$F'(x) = \frac{1}{3600x^5(x+1)^2(2x^2-\ln x - \ln 2\pi + 2x+1)}(q_2(\ln x)^2 + q_1\ln x + q_0)$$ where \begin{align} q_2 &= 3600x^4+1800x^3, \\ q_1 &= (7200\ln 2\pi - 9000)x^4 + (3600\ln 2\pi - 900)x^3 - 607x^2 - 2764x - 47, \\ q_0 &= -9000x^5 + (3600\ln^2 2\pi - 9000\ln 2\pi -2386)x^4 +(1800\ln^2 2\pi - 900\ln 2\pi+5842)x^3\\ &\quad +(-607\ln 2\pi + 6229)x^2 + (-2764\ln 2\pi + 2858)x - 47\ln 2\pi +47. \end{align} It is easy to prove that $q_2, q_1 > 0$ for $x\ge 1$. Since $x > \ln^2 x$ and $x > \ln x$ for $x\ge 1$, we have $$q_2(\ln x)^2 + q_1\ln x + q_0 < q_2 x + q_1 x + q_0, \quad \forall x\ge 4.$$ It is easy to prove that $q_2 x + q_1 x + q_0 < 0$ for $x \ge 4$. Thus, we have $F'(x) < 0$ for $x\ge 4$. Note also that $\lim_{x\to \infty} F(x) = 0$. Thus, we have $F(x) > 0$ for $x \ge 4$. This completes the proof of Fact 6.
This does not answer the question completely, but proves the inequalities for large enough $n$.
Let $f(x)=e^{g(x)}$ where $g(x)=\frac{1}{x}\log\Gamma(x+1)$, and $h(x)=\left(\frac{x}{x+1}\right)^x$.
It is enough to show that $$\frac{x}{x+1}h(x)<f'(x)<h(x),$$
since $f(n+1)-f(n)=f'(c_n)$ for some $n< c_n <n+1$ by the Mean Value Theorem.
We use a version of Stirling's approximation of $\Gamma$ function:
$$\log\Gamma(x+1)=x\log x-x+\frac{1}{2}\log(2\pi x)+\sum_{n=1}^\infty \frac{B_{2n}}{2n(2n-1)x^{2n-1}}$$
This yields the following asymptotic relations for large enough $x$.
$$g(x)=\log x-1+\frac{\log(2\pi x)}{2x}+O(\frac{1}{x^2}),$$ $$g'(x)=\frac{1}{x}+\frac{1}{2x^2}-\frac{\log(2\pi x)}{2x^2}+O(\frac{1}{x^3}),$$ $$f'(x)=e^{g(x)}g'(x)=\frac{1}{e}(1+\frac{1}{2x}-\frac{\log^2(2\pi x)}{8x^2}+O(\frac{\log x}{x^2})),$$ $$h(x)=\frac{1}{e}(1+\frac{1}{2x}+O(\frac{1}{x^2})),$$ $$\frac{x}{x+1}h(x)=\frac{1}{e}(1-\frac{1}{2x}+O(\frac{1}{x^2}))$$
Thus, we have the claim for large enough $x$, and this proves the inequalities for large enough $n$.
Remark1) Treating error terms extra carefully might give an explicit $N$ such that the inequalities hold for $n>N$.
Remark2) Once we find such $N$, we can check one by one for $n=1,2,\cdots N$.
Here is a partial answer :
If a sequence $u=(u_n)_{n\ge1}$ of real numbers converges, then the sequence $\left(\frac{1}{n}\sum_{k=1}^nu_k\right)_{n\ge1}$ converges to the same limit. This is the well known Cesaro's lemma.
It can be proved that the converse is false (consider the sequence $u=((-1)^n)_{n\ge1}$) but becomes true if we assume that $u$ is monotonic.
As a consequence, we get the following result :
If $t=(t_n)_{n\ge1}$ is a monotonic sequence of real numbers such that $\lim_{n\to\infty}\frac{u_n}{n}=L\in\mathbb{R}$ then $\lim_{n\to\infty}\left(u_{n+1}-u_n\right)=L$.
Let's apply this last result to the sequence $t=(\left[n!\right])^{1/n})_{n\ge1}$.
It's easy to show ($\color{red}{\mathrm{see}\,\,\mathrm{below}}$) that
$$\lim_{n\to\infty}\frac{\left[n!\right]^{1/n}}{n}=\frac{1}{e}$$
Therefore, if we prove that $t$ is monotonic (at least ultimately, which is a sufficient condition), we will reach the conclusion that :
$$\lim_{n\to\infty}\left(\left[(n+1)!\right]^{1/(n+1)}-\left[n!\right]^{1/n}\right)=\frac{1}{e}$$
It is a consequence of Cesaro's lemma that if a sequence of positive real numbers $(x_n)_{n\ge1}$ verifies $\lim_{n\to\infty}\frac{x_{n+1}}{x_n}=L$ some $L>0$ then $\lim_{n\to\infty}\left(x_n\right)^{1/n}=L$.
Applying this to sequence $x_n=\left(\frac{n!}{n^n}\right)$ we obtain $\lim_{n\to\infty}\frac{\left[n!\right]^{1/n}}{n}=\frac{1}{e}$
By partial summation: $$\sum_{j=1}^{n}\log j = n\log n - n + \sum_{j=1}^{n}\left(1-j\log(1+1/j)\right),$$ so it is possible to fix @i707107's argument (removing "for any $N$ big enough") by noticing that $$\left(1-j\log(1+1/j)\right) \in \left(\frac{1}{2j},\frac{1}{2j+2}\right).$$
Could one go from large $x$ (the case already treated in @SungjinKim 's answer) back to smaller $x$? In principle yes, but I do not know how difficult it would be to show that a certain derivative is negative (if it is...might be naive to expect this would be any easier than the original problem, but I am curious). For example, let
$L(n)=\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}-(\frac n{n+1})^{n+1}$ and
$L(x)=\sqrt[x+1]{\Gamma(x+2)}-\sqrt[x]{\Gamma(x+1)}-(\frac x{x+1})^{x+1}$ , for $x>0$.
If $L'(x)<0$ for all $x>0$ and if $L(x)>0$ for large enough $x$ then $L(x)>0$ for all $x>0$ (which would show the first of the two OP inequalities $(\frac n{n+1})^{n+1}<\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\ $).
I didn't do much re this new question (not an answer), apart from asking wolfram alpha, which gave a plot of $L'(x)$ which looks like a negative function indeed.
Just for the sake of avoiding $x+2$ in the expression (at the expence of introducing $x-1$), one may also wish to consider
$G(x)=L(x-1)=\sqrt[x]{\Gamma(x+1)}-\sqrt[x-1]{\Gamma(x)}-(\frac{x-1}x)^x$ , for $x>1$
Similarly, one may introduce
$R(x)=(\frac x{x+1})^x-\sqrt[x+1]{\Gamma(x+2)}+\sqrt[x]{\Gamma(x+1)}$
and try to show that its derivative is negative for $x>0$.
(Or work instead with $R(x-1)=(\frac{x-1}x)^{x-1}-\sqrt[x]{\Gamma(x+1)}+\sqrt[x-1]{\Gamma(x)}$, for $x>1$).
"Confirmed" by wolfram alpha for $0<x<60$:
https://www.wolframalpha.com/input/?i=derivative+of+%28+%28x%2F%28x%2B1%29%29%5Ex-%28Gamma%28x%2B2%29%29%5E%281%2F%28x%2B1%29%29%2B%28Gamma%28x%2B1%29%29%5E%281%2Fx%29+++++%29+for+x+from+0+to+60
Computing some values (with Reduce computer algebra) it seems that the second of the two inequalities (i.e. $\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}<(\frac n{n+1})^n\ $) is a bit tighter than the first one ($(\frac n{n+1})^{n+1}<\sqrt[n+1]{(n+1)!}-\sqrt[n]{n!}\ $), (but that both hold true).
I feel I have no idea what I am talking about (and that I didn't do much by just posting a couple of links to wolfram alpha) so I post this as community wiki. (I read a little bit about the derivative of $\Gamma(x)$ on wikipedia and it looks like I need to learn a bit more to be able to follow.)
Also from wolfram alpha:
https://www.wolframalpha.com/input/?i=derivative+of+%28+%28x%2F%28x%2B1%29%29%5Ex-%28Gamma%28x%2B2%29%29%5E%281%2F%28x%2B1%29%29%2B%28Gamma%28x%2B1%29%29%5E%281%2Fx%29+++++%29+
$\frac d{dx}\bigl((\frac x{x + 1})^x-\Gamma(x+2)^{\frac 1{x + 1}}+\Gamma(x+1)^{\frac1x}\bigr)=$
${(\Gamma(x+1))}^{\frac1x}
\bigl(
\frac{\psi^{(0)}(x+1)}x-
\frac{\log(\Gamma(x+1))}{x^2}
\bigr)+$
$\ (\frac x{x + 1})^x
\bigl(
(x+1)
(\frac1{x + 1}-\frac x{(x+1)^2})+
\log(\frac x{x + 1})
\bigr)-$
$\ \ (\Gamma(x+2))^{\frac 1{x + 1}}\bigl(\frac{\psi^{(0)}(x+2)}{x+1}-
\frac{\log(\Gamma(x + 2))}{(x + 1)^2}\bigr)$
Just some remark :
We have $x>1$ and $\exists a,0<a<1$:
$$f\left(x\right)=x^{\frac{x}{x+1}},g\left(x\right)=1+x-\sqrt{x},h(x)=\left(\sqrt[x+1]{(x+1)!}-\sqrt[x]{x!}\right)^{\frac{1}{2x+1}},t(x)=\left(\sqrt[x+1]{(x+1)!}-\sqrt[x]{x!}\right)^{a}\left(\left(\sqrt[x+1]{(x+1)!}-\sqrt[x]{x!}-1\right)\left(\frac{1}{2x+1}-a\right)+1\right)$$
Then it seems we have :
$$f\left(\frac{x}{x+1}\right)\geq g\left(\frac{x}{x+1}\right)\geq t(x)\simeq h(x)$$
Where :
$$\frac{\left(\frac{1}{a}-1\right)}{2}\simeq x$$
Now it seems we have $x>1$:
$$2\frac{\left|\left(\sqrt[x+1]{(x+1)!}-\sqrt[x]{x!}\right)^{\frac{1}{2x+1}}-\frac{\sqrt[x+1]{(x+1)!}}{\sqrt[x]{x!}}\right|}{x^{2}}\geq \left|\left(\sqrt[x+1]{(x+1)!}-\sqrt[x]{x!}\right)^{\frac{1}{2x+1}}-g\left(\frac{x}{x+1}\right)\right|$$
Then there is a possibility to use Gautschi's inequality and their refinements
For a start with Hm-Gm see Does three iteration are sufficient to use Newton's method
