16

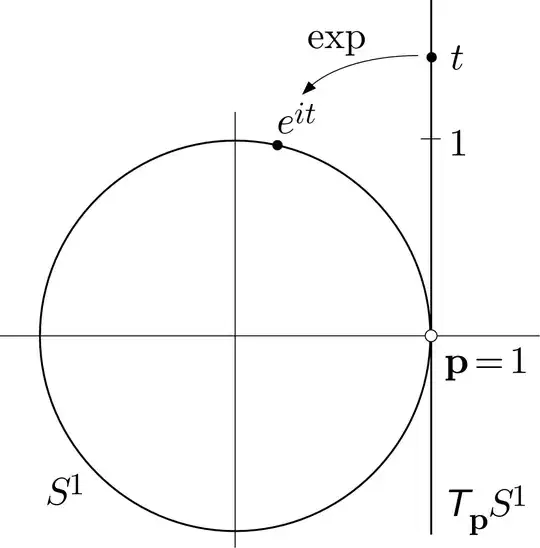
The exponential map $exp_{p}:T_{p}M \to M$ given a suitable $v \in T_{p}M$, returns $p$, displaced along the geodesic uniquely determined by $(p,v) \in TM$ for unit "time".

So, what does the above have to do with the familiar concept/s of exponentiation?
Why does this map carry this name?

user76568
  • 4,542
  • 4
    In the case of matrix groups, it really is the matrix exponential. –  Jan 10 '14 at 08:39

2 Answers2

21

Look at the following figure (from an analysis textbook). For more background, in particular in connection with Lie algebras/groups see the Wikipedia article about the exponential map. The exponential series does indeed appear there.

enter image description here

Christian Blatter
  • 226,825
6

The function $f(t)=\mathrm{e}^{at}$ can be viewed as the solution of the initial value problem: $$ x'=ax, \quad x(0)=1. $$ More generally, if $A\in\mathbb R^{n\times n}$ and $u_0\in\mathbb R^n$, then the solution of the initial value problem: $$ x'=Ax, \quad x(0)=u_0, $$ is $u(t)=\mathrm{e}^{tA}u_0$, where $\mathrm{e}^{tA}$ is the exponential of the matrix $A$. It $A$ possessed imaginary eigenvalues, then $u(t)$ returns to a multiple of itself, for suitable initial $u_0$.

Yiorgos S. Smyrlis
  • 83,933
  • 1
    You could be a bit more concrete about what the underlying manifolds are for which this makes the connection to the differential geometric definition – Bananach Sep 13 '18 at 10:29