16

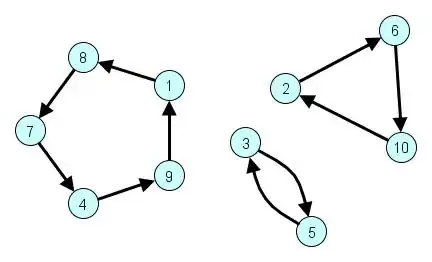
I have attempted a proof of this, but upon looking at my notes, I feel it might be incorrect: it is noticeably simpler than the one in my notes.

Proposition: any permutation in $S_n$ can be written as a product of disjoint cycles.

Proof (attempt): $s\in S_n$. Let $\langle s\rangle$ act on $X=\{1,\cdots,n\}$. Define $x\sim x'\iff x'\in\text{Orb}(x)$ for $x,x'\in X:$ this is clearly an equivalent relation, hence the orbits partition $X$. Each orbit corresponds a cycle in $s$, so we are done.

Does this hold, or have I missed something vital?

Martin Sleziak
  • 53,687
user118224
  • 1,509

2 Answers2

17

The proof is indeed correct. There is a nice intuition behind this:

You can interpret a permutation as a directed graph: The nodes are the numbers $1,\dots,n$ and there is an arrow from $a$ to $b$ if the permutation $\pi$ maps $\pi(a)=b$. This is a functional graph and as the number of nodes is finite and the map is one-to-one, every node has exactly one in-edge and exactly one out-edge. It is clear that this graph must be a set of disjoint cycles (hence the name).

Of course this is only a picture to the proof, to show where it comes from. The proof is correct because we can easily check that $S_n$ indeed acts on $X$ and orbits are cycles.

EDIT: Someone requested a real picture, not only a sketch of the proof. So I add one showing the corresponding graph of the permutation $\left(\begin{eqnarray} 1&2&3&4&5&6&7&8&9&10 \\ 8&6&5&9&3&10&4&7&1&2 \end{eqnarray}\right)$.

enter image description here

benh
  • 6,605
  • What happened to the picture that you mention in your last paragraph? Can it be linked or uploaded back? –  Jan 19 '14 at 07:24
  • @FrankMuer I meant a sketch, not a picture. Sorry for using the wrong word. I added a picture in order to make it correct. – benh Jan 19 '14 at 15:13
  • Exquisite picture. Thanks a lot. Upvoted. No problem. What'd you flesh it out with? –  Jan 20 '14 at 13:25
  • 1
    @FrankMuer Thanks, that's yEd graph editor. – benh Jan 28 '14 at 12:35
7

If, in proving this theorem, you have available the previously explained notion of group-actions and orbits, and if you have defined "cycles" in this manner, then yes your proof is valid. However, in the progression of a typical algebra course, this theorem is covered before those "tools" are available, hence the need for a more "complicated" proof.

Ben Grossmann
  • 225,327