11

How would I calculate the power series of $f(x)$ if $f(f(x)) = e^x$? Is there a faster-converging method than power series for fractional iteration/functional square roots?

Gottfried Helms
  • 34,920
jnm2
  • 3,170
  • Are you looking for an analytic function? Such a $f$ does not exist in the analytic category. – Henri Aug 22 '11 at 16:03
  • I wasn't aware that $f$ wasn't analytic, but I'm looking for whatever I can graph. – jnm2 Aug 22 '11 at 16:05
  • 2
    Aside: $f$ cannot be a function composed of basic arithmetic operations, exponentials, and logs: Scott Aaronson has a proof here (see Comment #52), that for any such function, $f(f(x))$ is either subexponential or superexponential. See also Mathoverflow where it is said that "there are analytic solutions in a neighborhood of the real line, but they are known not to be entire". – ShreevatsaR Aug 22 '11 at 16:06
  • 3
    Also an answer at the above Mathoverflow question links to these discussions which are about precisely your question. – ShreevatsaR Aug 22 '11 at 16:07
  • @Henri: An explanation of why no such analytic function can exist would probably be a good answer, even though it does not completely answer the question. – Michael Hardy Aug 22 '11 at 17:27
  • See http://math.stackexchange.com/questions/3633/square-root-of-a-function-in-the-sense-of-composition – Álvaro Lozano-Robledo Aug 22 '11 at 17:37
  • @Michael Hardy: Ok, I'll post such an answer soon. – Henri Aug 22 '11 at 18:27
  • @Gottfried, the question, though related, doesn't exactly deal with tetration per se, yes? – J. M. ain't a mathematician Aug 25 '12 at 15:05
  • @J.M.: hmm, isn't that search for a power-series for the half-iterate of the exponentiation the beginning of the search for the general-iterate? This is just how I understood the question...(but it may as well be that I'm aside of the common understanding of tetration in mse - should we better open a chat?) – Gottfried Helms Aug 25 '12 at 15:28

3 Answers3

15

Look at this answer:

https://mathoverflow.net/questions/17605/how-to-solve-ffx-cosx/44727#44727

In short, the analytic solution is

$$g^{[1/2]}(x)=\phi(x)=\sum_{m=0}^{\infty} \binom {1/2}m \sum_{k=0}^m\binom mk(-1)^{m-k}g^{[k]}(x)$$

$$g^{[1/2]}(x)=\lim_{n\to\infty}\binom {1/2}n\sum_{k=0}^n\frac{1/2-n}{1/2-k}\binom nk(-1)^{n-k}g^{[k]}(x)$$

$$g^{[1/2]}(x)=\lim_{n\to\infty}\frac{\sum_{k=0}^{n} \frac{(-1)^k g^{[k]}(x)}{(1/2-k)k!(n-k)!}}{\sum_{k=0}^{n} \frac{(-1)^k }{(1/2-k) k!(n-k)!}}$$

Insert here $g(x)=a^x$ The same way you can find not only square iterative root but iterative root of any order. Unfortunately this does not converge for $g(x)=a^x$ where $a > e^{1/e}$.

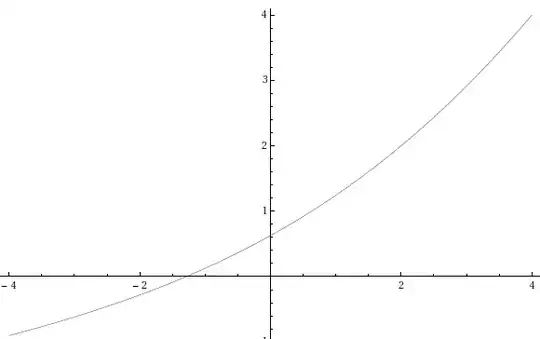
Here is a graphic for iterative root of $g(x)=(\sqrt{2})^x$ http://static.itmages.ru/i/10/1106/h_1289022627_2dd67c314b.png

The question becomes more difficult when speaking about the base $a>e^{1/e}$. But in this case the solution can also be constructed, see this article.

Community
  • 1
Anixx
  • 9,119
  • How can you compute a solution for $a=\sqrt2$ while you wrote " (...) does not converge where $a \le e^{1/e}$ (...)" ? And how can we approximate a solution when in the third formula high iterates of $g(x)$ are required and the base is greater than $e^{1/e}$ ? – Gottfried Helms Dec 25 '14 at 12:37
  • @Gottfried Helms typo. It does not converge when $a > e^{1/e}$, of course. – Anixx Dec 25 '14 at 13:24
  • I see. (big relief!) Thank you for clarification. P.s. Did you know that I made a comparision between the computation which you called the Newton-series (when I did it I didn't know that my computations were equivalent to that) and an approach which involves diagonalization? In that discussion the diagonalization-approach was characterized by the property that it converges to the same solution, but much faster (with less terms). If you're interested: http://go.helms-net.de/math/tetdocs/index.htm , see the third entry "comparision of two methods" – Gottfried Helms Dec 25 '14 at 15:02
10

Here's the proof of a theorem due to Thron (1956), extracted from a article of Laurent Bonavero (available at his webpage).

Theorem. There is no entire function $f$ (that is $f:\mathbb C \to \mathbb C$ holomorphic) such that $\exp = f \circ f$.

Proof. If such a function $f$ exists, then $f(\mathbb C)= \mathbb C^*$. Indeed, $f(\mathbb C) \supset \exp(\mathbb C) = \mathbb C^*$, but $0$ can't be in the image of $f$: if $f(x)=0$, then as $x \neq 0$, there exists $y$ such that $x=f(y)$ so that $\exp(y)=0$, absurd.

Therefore $f$ can be lifted by the exponential, $f=\exp \circ g \,$ for $g$ entire. So $\exp = \exp(g \circ f)$, and there must exist a constant $C$ such that $g \circ f(z)=z+C$ for all $z\in \mathbb C$. It follows that $f$ is injective, so $\exp$ should be injective too, which is absurd!

Henri
  • 1,164
3

There is a lot of material about this question here and in mathoverflow. There is also a "Tetration forum", where someone has implemented a version of tetration due to Hellmuth Kneser, see some forum entries there: http://math.eretrandre.org/tetrationforum/forumdisplay.php?fid=8" also in citizendium there is an extensive article of Dmitri Kousznetzov who claims he has a usable interpretation (and implementation) see http://en.citizendium.org/wiki/Tetration

Gottfried Helms
  • 34,920