Examples of rings with ideal lattice isomorphic to $M_3$, $N_5$

Question

In thinking about this recent question, I was reading about distributive lattices, and the Wikipedia article includes a very interesting characterization:

A lattice is distributive if and only if none of its sublattices is isomorphic to $M_3$ or $N_5$.

where
$\hskip 1.7in$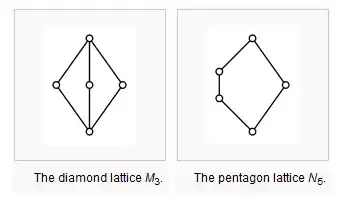

As the answers to the other question demonstrate, it is pretty easy to construct examples of rings with non-distributive ideal lattices; for example, any Noetherian domain either having Krull dimension $>1$, or being non-integrally closed, has a non-distributive ideal lattice. For example, true to the above characterization, the lattice of ideals of $k[x,y]$ has an $M_3$ sublattice: $$(x,y)$$ $$\text{ / }\qquad |\qquad \text{ \ }$$ $$\quad\quad(x)\quad\quad(y)\,\,\,\,\quad (x+y)$$ $$\text{ \ } \qquad |\qquad \text{ / }$$ $$(0)$$ Of course, it has many other such sublattices, and even in the above example, there are other ideals like $(x+2y)$, $(x^2)$, etc. that live between $(0)$ and $(x,y)$, that we have thrown out for the purposes of getting our $M_3$ sublattice. What I would like to see are examples both of a ring having an ideal lattice isomorphic to $M_3$, and a ring having ideal lattice isomorphic to $N_5$. (I take my rings to be commutative unital rings, and I want to consider the lattice of ideals as including $R=(1)$.) As I mentioned, there are other ideals between $(0)$ and $(x,y)$, so getting a ring with an $M_3$ ideal lattice is not as easy as localizing $k[x,y]$ at $(x,y)$.

My best shot at producing a ring with an $M_3$ ideal lattice was $R=\mathbb{F}_2[x,y]/(x,y)^2$, which has $$R$$ $$|$$ $$(x,y)$$ $$\text{ / }\qquad |\qquad \text{ \ }$$ $$\quad\quad(x)\quad\quad(y)\,\,\,\,\quad (x+y)$$ $$\text{ \ } \qquad |\qquad \text{ / }$$ $$(0)$$

So, what are some good examples of rings having ideal lattice isomorphic to $M_3$? What about $N_5$?

Answer 1

There are no such rings.

A commutative ring with finitely many ideals is artinian. A commutative artinian ring is a direct product of artinian local rings. The direct product of n local rings has n maximal ideals, so you know n = 2 or 3. However, the lattice of a direct product is a type of lattice product, and the lattices you give are not such products (since they are so small, just check all lattices of the appropriate cardinality).

For the particular lattices you are looking at, there is a counting argument: If R, S are rings, then the ideals of R × S are all I × J for ideals I and J of R and S respectively. In particular, if a commutative ring had M₃ as an ideal lattice, then it would be a direct product of three artinian local rings, and so one could write 4 as a product of three positive integers greater than 1. If a commutative ring had N₅ as an ideal lattice, then 5 would be a product of two positive integers greater than 1.

Answer 2

I know the original question was about commutative rings, but I just wanted to include in this post that there is a cute example if you allow noncommutative rings.

In $R=M_2(\mathbb{F}_2)$ (the 2 by 2 matrix ring with entries from the field of two elements) there are exactly five right ideals, and they form the lattice $M_3$. (The same can be said for the left ideals.)

Because $R$ is semisimple each right ideal is generated by an idempotent. One can check there are 6 nontrivial idempotents, but actually it turns out they pair off and they only generate three different ideals. These ideals are: $$\begin{pmatrix}1&0\\0&0\end{pmatrix}R, \begin{pmatrix}0&0\\0&1\end{pmatrix}R, \begin{pmatrix}0&1\\0&1\end{pmatrix}R $$

One should not forget to check that their pairwise intersections are $\{0\}$ and that their pairwise sums are $R$!

Answer 3

Consider $R=\mathbb F_2[x,y]/(x^2,xy,y^2)$. This is local, and the maximal ideal is $\mathfrak{m}=(x,y)R$, a $2$-dimensional $\mathbb F_2$ vector space, whose subspaces are precisely the ideals of $R$. Because the base field is very small, there are exactly five such subspaces.