5

Why is it that when one in considering contour integration of a real function, such as $$ \int_{-\infty}^{\infty} \frac{dx}{1+x^2}$$ the contour in the complex plane used is the following:

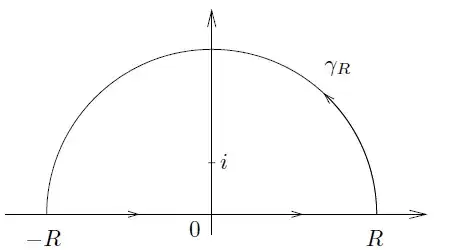
enter image description here

Furthermore, what are the general strategies for choosing a contour when integrating a real function using the method of residues? For example, what contour would be used for the function $$\int_{0}^{\infty} \frac{dx}{1+x^2}.$$ Or for the function $$\int_{0}^{\pi} \frac{d \theta}{(a+b \cos\theta)^2}.$$ (Notice how the limits of integration changed). I am also curious how the position of the residues in $\mathbb{C}$ affect a contour. My complex analysis book tends to pull a contour out of thin air with out any appeal to intuition. Any help would really be great! Thank you.

Eric
  • 1,821

2 Answers2

2

Well, the reasoning behind the semi-circle contour is that $$\int_{0}^{\pi} \frac{1}{1+re^{it}}\cdot \frac{1}{ire^{it}} dt \rightarrow 0$$ as $r \rightarrow \infty$.

However, $$\oint_{\gamma} \frac{1}{1+z^2} dz = 2\pi i\cdot \frac{1}{2i} = \pi.$$

Hence, $$\text{lim}_{x \rightarrow \infty}\int_{-x}^{x}\frac{1}{1+t^2} dt = \pi - 0 = \pi.$$

As for choosing a contour, in the first case, it is the exact same as your first problem. Since $\frac{1}{1+x^2}$ is even $\text{lim}_{x \rightarrow \infty}\int_{0}^{x}\frac{1}{1+t^2} dt = 1/2\cdot \text{lim}_{x \rightarrow \infty}\int_{-x}^{x}\frac{1}{1+t^2} dt = \pi/2$. In the second case, try substituting $cos(t) = 1/2\cdot (e^{it}+e^{-it})$. As for general methods, it comes from practice and seeing many problems more than anything. It is very much like developing the intuition for integration techniques.

Christopher K
  • 3,383
2

I think it's hard to make a general statement, but in many cases, the contour that you've shown above is good because the portion of the semicircle lying along the real axis gives us the integral we want (when we take $R$ to be very large), and the circular portion of the contour can be easily integrated on and shown to tend to zero for large $R$. It's not necessarily that you couldn't choose something else, but we understand (in many cases like these) how to integrate along circular contours well.

There is no one size fits all method, though. Different contours will lend themselves well to different situations. For example, if you a residue which lies on the real axis, you might have to use a contour which uses a different fraction of a circle - say, in some cases a third circle. In other cases, you might have to avoid a branch cut, and can use an annular region. Experience and clever choices will dictate what contours are best.

In one of your specific cases, for example, the integral

$$\int_{0}^{\infty} \frac{dx}{x^{2}+1}$$

can be integrated by using the contour given, and then observing that $\frac{1}{x^{2}+1}$ is an even function.

Alex Wertheim
  • 20,278