I would recommend to implement some transformations of the integral first.
For example,
$$I=\int_{-\infty}^\infty\frac{dw}{1+iw^3}=-i\int_{-\infty}^\infty\frac{dw}{w^3-i}=-i\int_{0}^\infty\frac{dw}{1+iw^3}-i\int_{-\infty}^0\frac{dw}{1+iw^3}$$
Making change in the second integral $t=-w$
$$I=-i\Big(\int_{0}^\infty\frac{dw}{w^3-i}-\int_{0}^\infty\frac{dw}{w^3+i}\Big)=2\int_{0}^\infty\frac{dw}{w^6+1}$$
Now, we can go different ways.
For example, this one:
$$I=2\int_{0}^\infty\frac{w^5dw}{w^5(w^6+1)}=\frac{2}{6}\int_{0}^\infty\frac{d(w^6)}{w^5(w^6+1)}=\frac{1}{3}\int_{0}^\infty\frac{t^{-5/6}}{(t+1)}dt$$
Taking a keyhole contour in the complex plane with the cut from zero along the positive part of axis $X$ (we need it to make the function single-valued).
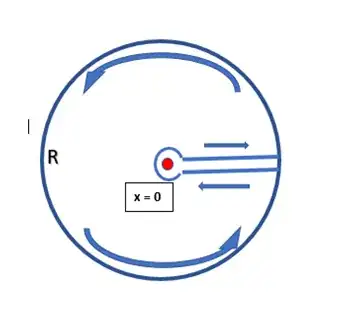
Integral along a big circle $\to0$ as $R\to \infty$ (function decreases rapidly enough). Also, integral along a small circle (around zero) $\to0$ as $r\to0$.
Integral along the upper bank of the cut is the desired integral $I= \frac{1}{3}\int_0^\infty\frac{z^{-5/6}}{z+1}dx$
And integral along the lower bank of the cut is integral $-Ie^{2\pi i(-5/6)}$ (minus is due to integration in the negative direction, and the factor $e^{2\pi i(-5/6)}$ - due to the full turn counter-clockwise around the branch point $z=0$)
You will get $I(1-e^{2\pi i(-5/6)})=2\pi i \,Res _{(z=e^{\pi i})}\frac{1}{3}\frac{z^{-5/6}}{z+1}=\frac{2\pi i}{3}e^{-5\pi i/6}$ - residual in one simple pole inside the contour.
Finally,
$$I=\frac{1}{3}\frac{2\pi i}{e^{5\pi i/6}-e^{-5\pi i/6}}=\frac{\pi}{3\sin(5\pi/6)}=\frac{2\pi}{3}$$
In another way we can evaluate this integral via beta-function. Making change $x=\frac{1}{1+t}$
$$I=\frac{1}{3}\int_{0}^\infty\frac{t^{-5/6}}{(t+1)}dt=\frac{1}{3}\int_0^1\frac{(1-x)^{-5/6}x}{x^{-5/6}x^2}dx=\frac{1}{3}\int_0^1(1-x)^{-5/6}x^{-1/6}dx$$
$$=B\big(1/6;5/6\big)=\frac{\Gamma(1/6)\Gamma(5/6)}{\Gamma(1/6+5/6)}$$
Using Euler reflection formula $\Gamma(x)\Gamma(1-x)=\frac{\pi}{\sin(\pi x)}$
$$I=\frac{1}{3}\frac{\pi}{\sin(5/6)}=\frac{2\pi}{3}$$
