Angle between lines joining tetrahedron center to vertices

Question

What are the angles formed at the center of a tetrahedron if you draw lines to the vertices?

I'm trying to make these:

I need to know what angles to bend the metal.

Answer 1

The required tetrahedral angle is $\arccos\left(-\frac13\right)\approx109.5^\circ$. You can use the law of cosines to show this... or more transparently, you can exploit the fact that a tetrahedron is easily embedded inside a cube:

---

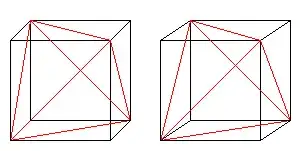
I suppose now's as good a time as any to post the synthetic proof.

One can use the Pythagorean theorem to show that a square with unit edge length has a diagonal of length $\sqrt 2$. The Pythagorean theorem can be used again to show that a right triangle with leg lengths $1$ and $\sqrt 2$ will have a hypotenuse of length $\sqrt 3$ (corresponding to the triangle formed by an edge, a face diagonal, and a cube diagonal). We know that the diagonals of a rectangle bisect each other; this can be used to show that the diagonals of a cube bisect each other. From this, we find that the side lengths of the (isosceles!) triangle formed by two half-diagonals of the cube (corresponding to two of the arms of your caltrops) and a face diagonal are $\frac{\sqrt 3}{2}$, $\frac{\sqrt 3}{2}$, and $\sqrt{2}$. From the law of cosines, we have

$$2=\frac34+\frac34-2\frac34\cos\theta$$

where $\theta$ is the obtuse angle whose measure we are seeking. Algebraic manipulation yields $\cos\,\theta=-\frac13$.

Answer 2

One way is to write the vertices as vectors $a,b,c,d$ with norm $\|\cdot\|=1$. Then $a+b+c+d=0$. But

$$ 0=\|a+b+c+d\|^2=4+2{4 \choose 2}\cos\theta,$$

so $\theta = \arccos(-1/3)$.

Answer 3

(Assuming the tetrahedron is supposed to be regular) Take the tetrahedron with vertices $(1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1)$, which has centre at the origin, and use the dot product formula:

$a\cdot b = |a| |b|\cos\theta$

which gives $\cos\theta=-\frac13$

Answer 4

The angle is $$\theta = \arccos \left(-\frac{1}{3}\right) \approx 109.47.$$ You can find this angle by writing the volume of a regular tetrahedron in two different ways.

(this is an adaptation of a blog post I wrote for a website that has since been deleted)

---

For setup, here is a picture of the regular tetrahedron in question:

If we knew the vertical distance, $h$, from the base of the tetraheron to the center, then we could find the angle to be $$\theta = \arccos \left(-h\right).$$ This follows from basic 2D trigonmetry, as shown in the following diagram which views the tetrahedron from the side:

We can find $h$ in a roundabout way by, taking advantage of the symmetry of the tetrahedron. Break the big tetrahedron into 4 smaller tetrahedra:

Now we may use the formula $\text{volume} = \frac{1}{3} \times \text{base} \times \text{height}$ on the smaller tetrahedra, and the larger tetrahedra, to come up with two different expressions for the volume. Then, we can set these two expressions equal, solve for $h$, and plug the result into the previous formula to get the desired angle:

---

One may trivially extend this argument to regular simplices of arbitrary dimension. There one would break an $n$-simplex into $n+1$ equal pieces, therefore yielding the angle $$\theta = \arccos \left(-\frac{1}{n}\right).$$

Answer 5

If the tetrahedron is regular, we can use statical equilibrium of four equal isotropic forces with angle $ \theta$ between any two of them. Referencing with reference to any one force,

$$ F \cos \theta + .. + .. + F = 0$$

$$ \cos \theta = -\frac13 $$

To generalize for all $i$ direction forces on a particular Z direction the vector dot product sum can be used:

$$ \Sigma F_i . Z =0 $$

Answer 6

Using the illustration of the tetrahedron embedded into the cube, you can lay out some dimensions. Assign a length of 2 to the sides of the cube, and then according to an old guy name Pythagoras, the hypotenuse of each side will be d 2*√2. Since the center of the tetrahedron is also the center of the cube, then you can draw an isosceles triangle using the hypotenuse and the center that will be 2*√2 at the base and 1 unit high. Split that in half to make two right triangles, each with a base of √2 and a height of 1. Now comes the real trig. Tan = Opposite / Adjacent, or √2/1, or just √2. Grab your calculator and you'll find that the angle you're looking for a the top of the right triangle is 54.735°. Put those two triangles back together, and you get an angle of 109.47°. For fabrication, I think you'd be fine with an angle of 110°.

Answer 7

Consider a sphere passing through the four vertices of the regular tetrapod with it's centre at the centre of the tetrapod. Each set of three vertices form four congruent equilateral spherical triangles on the surface of the sphere. For a spherical triangle ABC (unlike plane triangles),

1. The sides a,b,c are also measured as angles subtended at the centre of the sphere.
2. $\pi <A+B+C<3\pi$ Here $A=B=C=120°$ and $a=b=c$ The required angle between any two arms is thus the measure of any side of any of the triangles. Cosine rule for spherical triangles $$\cos A= -\cos B. \cos C + \sin B. \sin C. \cos a$$ gives $$\cos a= -1/3$$ $$a= 109.47°$$

Answer 8

Another possible solution:

Consider the equilateral triangle, edge length x, formed by any 3 tips of a regular tetrapod (a face on it's corresponding tetrahedron).

The 3 medians of this equilateral triangle section it into 6 congruent right triangles with hypotenuse length y, and angles of 60° between lines around the centroid.

sin60° = (1/2x) / y

therefore

y = x / 2sin60°

Now consider a line running orthogonal to the previously identified triangle, from its centroid to the tip of the opposing tetrapod leg. This line is coincident with that opposing tetrapod leg and forms a right triangle with the previously identified y, having a hypotenuse equal in length to x.

Back to our tetrapod, any two legs form an isosceles triangle with base length x. Therefore, the angle between any two legs, A, can be expressed:

A = 180° - 2

where

= arcsin (y / x)

= arcsin ([x / 2sin60°] / x)

= arcsin (1 / 2sin60°)

therefore

A = 180° - 2[arcsin (1 / 2sin60°)]

A ≈ 109.47°

A more spatial approach, and certainly not the most direct, but it got me out of a pinch during a grade 12 chemistry test years ago. We were supposed to have the angles of molecular structures memorised and of course I blanked mid-test so I found myself deriving something to this effect in the margins.

This was on mobile so please forgive the formatting and lack of diagrams which surely would have made this explanation easier to follow.

Answer 9

Watch this Khan Academy video of Tetrahedral bond angle proof. In the video, Mathematical proof of the bond angles in methane (a tetrahedral molecule);

We have the tetrahedron structure, for example methane, which is a three-dimensional structure shown above. (It's very difficult to see tetrahedral geometry on a two-dimensional, But it's much easier to see it over here on the right with the three- dimensional representation of methane.)

The bond angle of sp3 hybridized carbon in methane is 109.5 degrees, so you could say that this angle is the same all the way around. orienting the tetrahedron in this way allows us to find the bond angle that we are going for.

And we don't know what bond angle yet, but we can figure out this angle right here. So I'm going to call this theta for this triangle that's formed. And I know that this distance down here is positive/negative square root of 2, and then we go up 1 on the y-axis and then 0 on the z-axis. And if I want to find my bond angle in here, those angles have to add up to equal 180 degrees.