How to cut a cube into an icosahedron?

Question

Edit: Originally I asked this about a using a cube, but it is not a requirement to start with a cube, just how to end up with an icosahedron as on of the answers showed how to make dodecahedron a having started ith any shape.

I have a cube, and I need to cut/file it into a icosahedron; what are the cut lines?

Same question for other Platonic solids: is it easy to start with a cube and get other shapes, Or is it better to choose a different solid as a starting point? I am asking this question from a physical/practical point; otherwise one can very well start with sphere (it is hard to file/cut a piece of wood/metal into a sphere).

Answer 1

Here are detailed instructions for cutting a tree stump into a regular dodecahedron. The essential trick is to make a template for the dodecahedron's dihedral angle. It should be possible to use similar techniques to make an icosahedron.

You might try practicing on fruit first: it's cheap and easy to cut.

Addendum: There are easy tricks for the tetrahedron and octahedron if you're starting with a cube. To get the octahedron, you just slice all the corners off: Mark the centers of three adjacent faces, cut in the plane that contains these three points, and you have cut one face of an octahedron. To get the tetrahedron, color the vertices of the cube in alternating colors, say red and black. Then on each face draw the diagonal from one red vertex to the other. These diagonals will form the edges of the tetrahedron; cut in planes that each contain three red vertices. To get the cube, cut nothing.

Answer 2

You can make a dodecahedron as follows:

Start with an octahedron $\mathcal O$ with edges of length $1$. You can color its faces inblack and white in such a way that no two faces of the same color share an edge, and then you can orient each edge of $\mathcal O$ so that when you move along it, with your head pointing towards the outside of $\mathcal O$, you have white on your left. Now pick a number $\theta\in[0,1]$ and on each edge of the octahedron mark the point which is at distance $\theta$ from the starting vertex of that edge (according tothe orientations we fixed)

If $\theta\in(0,1)$, then this construction gives us 12 points, one one each edge. If you think about this a little bit you'll see that for some value of $\theta$ these twelve points are the vertices of a dodecahedron: this is a simple consequence of the intermediate value theorem from calculus. One can explicitely compute this, with some work, and it turns out that we need $\theta$ to be the inverse of the golden ratio.

The following Mathematica code gives an interative thingie to see this construction:

vertex = Flatten[
   Map[NestList[RotateLeft, #, 2] & ,  {{1, 0, 0}, {-1, 0, 0}}, {1}], 
   1];
n = Length[vertex];
edges = Select[Subsets[vertex, {2}], 
   EuclideanDistance[#[[1]], #[[2]]] == Sqrt[2] &];
faces = Select[Subsets[vertex, {3}], 
   Complement[Subsets[#, {2}], edges] == {} &];
red = FindVertexCover[
   Graph[Rule @@@ 
     Select[Subsets[faces, {2}], 
      Length[Intersection[#[[1]], #[[2]]]] == 2 &]]];
orientedRedFaces = Map[Function[f, 
    Partition[
     If[Dot[Cross[f[[2]] - f[[1]], f[[3]] - f[[2]]], Total[f]] < 0, 
      f[[{1, 3, 2}]], f], 2, 1, 1]
    ], red];
orientedBlueFaces = Map[Function[f, 
    Partition[
     If[Dot[Cross[f[[2]] - f[[1]], f[[3]] - f[[2]]], Total[f]] < 0, 
      f[[{1, 3, 2}]], f], 2, 1, 1]
    ], Complement[faces, red]];
orientedEdges = Flatten[orientedRedFaces, 1];
Manipulate[
 Graphics3D[{
   Line /@ orientedEdges,
   {PointSize[0.02], 
    Point[t #[[1]] + (1 - t) #[[2]]] & /@ orientedEdges},
   FaceForm[Red],
   Polygon /@ 
    Map[t #[[1]] + (1 - t) #[[2]] &, orientedRedFaces, {2}],
   Polygon /@ 
    Map[(1 - t) #[[1]] + t #[[2]] &, orientedBlueFaces, {2}]
   }, Boxed -> False],
 {{t, 1/GoldenRatio, "\[Theta]"}, 0, 1}
 ]

This produces images such as

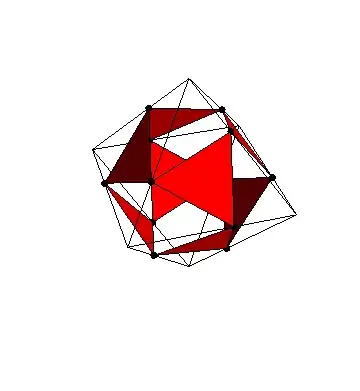
but the interesting thing is really the interactivity which allows you to play with it and see how the picture changes when you change $\theta$.

Now of course this does not answer your question, because I constructed a dodecahedron from an octahedron, and you wanted an icosahedron from a cube! But one can dualize this constructing, taking advantage of the fact that the dual of a cube is an octahedron, and the dual of an icosahedron is a dodecahedron. I'll leave all that fun to you.

Answer 3

Six of the thirty icosahedron edges and all twelve of its vertices lie on faces of the cube. Each icosahedron vertex lies near one cube edge and there is clearly the same number of icosahedron vertices as cube edges. $\dots$ Finally, from the model, observe that it is easy to list the $(x,y,z)$ coordinates of the twelve vertices:

• $(\pm 1 , \pm \phi, 0)$,
• $(0, \pm 1, \pm \phi)$, and
• $(\pm \phi, 0, \pm 1)$, where $\phi$ is the golden ratio.

from here.

Answer 4

A far easier method is to start with a cylinder. Measure the diameter and divide by 2. This is the pentagonal radius of the icosa. Divide this radius by 0.85065080352 to get the icosa side S ( figure out your own significant digits). Cut the cylinder length to 2 * S. Multiply the side length by 0.525731112119, this being the position of the side vertices from each end. This is where the pentagonal cross-section touches the side. Mark five points 72 degrees apart around the cylinder at the pentagonal plane. The second pentagonal cross-section is 36 degrees offset from the first set. Cut a flat plane between each set of three dots on the sides of the cylinder. Make a dot in the center of the ends of the cylinder. Cut from the pentagonal dot pairs to the end dot five times for each end.

Happy Icosa making !!!