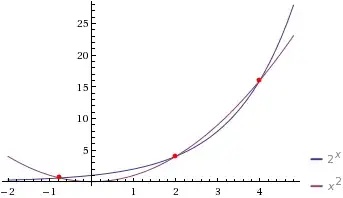
How many real roots are there to $2^x=x^2$?

Question

How many real roots are there to $2^x=x^2$?

Answer 1

An obvious solution is $x=2$.

If $2^x = x^2$, then $x\neq 1$ and $x\neq 0$. I'll treat the positive and negative cases separately.

If $x\gt 0$, then we get $x\ln(2) = 2\ln (a)$, or $\frac{x}{\ln x} = \frac{2}{\ln 2}$.

The derivative of $g(x) = \frac{x}{\ln x}$ is $\frac{\ln x - 1}{(\ln x)^2}$.

On $(1,\infty)$, the derivative is positive on $(e,\infty)$ and negative on $(1,e)$, so there is an absolute minimum at $x=e$, where the value is $e$; $\lim\limits_{x\to 1^+} g(x) = \lim\limits_{x\to\infty}g(x) = \infty$; since $\frac{2}{\ln 2}\gt e$, there are two values of $x$ where $g(x) = \frac{2}{\ln 2}$; one is $x=2$, which we had already found, the other is a value greater than $e$ (which as it happens is $4$).

On $(0,1)$, $g(x)$ is always negative, so there are no values where $g(x)=\frac{2}{\ln 2}$.

So for $x\gt 0$, there are two solutions.

For $x\lt 0$, the equation $2^x = x^2$ is equivalent to the equation $\left(\frac{1}{2}\right)^a = a^2$, where $a=-x\gt 0$. This time, the equation is equivalent to $\frac{a}{\ln a} = -\frac{2}{\ln 2}$. There are no solutions for $a\gt 1$, since $g(x)$ is positive there. On $(0,1)$, $g'(x)\lt 0$, so the function is strictly decreasing; we have $\lim\limits_{a\to 0^+}\frac{a}{\ln a} = 0$ and $\lim\limits_{a\to 1^-}\frac{a}{\ln a} = -\infty$, so there is one and only one value of $a$ for which $\frac{a}{\ln a} = -\frac{2}{\ln 2}$. Thus, there is one value of $x\lt 0$ which solves the equation.

In summary, there are three real solutions: one lies in $(-1,0)$, the second is $2$, and the third is $4$.

Answer 2

Explicitly, the third real solution (besides 2 and 4) is $- \frac{2 W(\ln(2)/2)}{\ln(2)}$, where $W$ is the Lambert W function.

Answer 3

Assuming that $x>0$, by taking logs of both sides and rearranging, we get that $$ \frac{\log(x)}{x}=\frac{\log(2)}{2} $$ Since $\frac{d}{dx}\frac{\log(x)}{x}=\frac{1-\log(x)}{x^2}$ vanishes only when $x=e$, and $\frac{\log(x)}{x}=\frac{\log(2)}{2}$ when $x=2$ and $x=4$, those are the only two positive solutions (i.e. the Mean Value Theorem says that $\frac{d}{dx}\frac{\log(x)}{x}$ vanishes between any two solutions).

For $x<0$, noting that $x^2=(-x)^2$, we have $$ \frac{\log(-x)}{x} = \frac{\log(2)}{2} $$ Since $\frac{d}{dx}\frac{\log(-x)}{x}=\frac{1-\log(-x)}{x^2}$ only vanishes at $x=-e$, there can be at most one solution in $(-e,0)$ and one in $(-\infty,-e)$.

For $x$ in $(-\infty,-e)$, $\frac{\log(-x)}{x}<0$ so there are no solutions in this range.

Since $\frac{\log(-(-1))}{-1}=0$ and $\frac{\log(-(-1/2))}{-1/2}=2\log(2)>\frac{\log(2)}{2}$, there must be a solution in $(-1,-\frac{1}{2})$, which is $x=-.766664695962123093111204422510$.

So to answer the question asked, there are three solutions.

Answer 4

Go to Wolfram|Alpha and type $2^x=x^2$ (link)

Answer 5

To flesh out Robert's solution:

$$x^2=\exp(x\ln 2)$$

can be rearranged as:

$$x^2 \exp(-x\ln 2)=1$$

Take the appropriate square root of both sides:

$$x \exp\left(-x\frac{\ln 2}{2}\right)=-1$$

multiply both sides with the appropriate factor:

$$-x \frac{\ln 2}{2}\exp\left(-x\frac{\ln 2}{2}\right)=\frac{\ln 2}{2}$$

invoke the Lambert function:

$$-x \frac{\ln 2}{2}=W\left(\frac{\ln 2}{2}\right)$$

and Bob's your uncle:

$$x=-\frac{2}{\ln 2}W\left(\frac{\ln 2}{2}\right)$$

Also,

$$-\frac{2}{\ln 2}W\left(-\frac{\ln 2}{2}\right)=2$$

and

$$-\frac{2}{\ln 2}W_{-1}\left(-\frac{\ln 2}{2}\right)=4$$

where $W_{-1}(x)$ is the other branch of the Lambert function that is real in the interval $[-1/e,0)$

Answer 6

you have 3 roots:

You can put your equation into a function:

$$f(x)=2^x-x^2$$

Now the question is, for what x is $f(x) = 0$; or, what are the roots of f(x)? The Newton-Raphson method starts with some first guess, $x_0$, and finds the next guess, $x_1$, by a formula. Then, using this guess, we apply the same formula to find a new guess, $x_2$. We continue until we're as close as we wish. The formula is

$$x_{i+1} = x_{i} - \frac{f(x_{i})}{f'(x_{i})}$$

We need $f'(x)$, the derivative of $f(x)$. It is

$$f'(x) = 2^x * ln(2) - 2x$$

Thus the formula for our problem is

$$x_{i+1} = x_{i} - \frac{(2^{x_i}-x^2)}{(2^{x_{i}}*ln(2)-2x)}$$

You can set this up in a spreadsheet. Then try different first guesses $x_0$. You'll find that the algorithm zeroes in on one of the three roots, depending on the starting value. If I start with $x_0 = 0$, I get the root:

$$x = -0.766664696$$

after 5 iterations. You can verify:

$$2^{-0.766664696} = 0.587774756$$ $$(-0.766664696)^2 = 0.587774756$$

If I start with $x_0 = 1$, I get the root $x=2$. If I start with $x_0 = 3$, I get the root $x = 4$. You have observed that there are three roots.

I hope this helps

Answer 7

By drawing the graphs of both functions, we can easily guess that there are three. What the roots actually are, I don't know, but at least I can answer your question.

To prove this, one might want to use Rolle's Theorem on the function $f(x) = 2^x - x^2$ to show the existence of the third $0$, which is the non-trivial one (the first two are $x=2$ and $x=4$). Just notice that $f(0) = 1$ and say $f(-100) < 0$, hence there exists a zero between those points. Since the derivative of $f$ is strictly positive in the interval $(-\infty, 0)$, this is the only one in this interval.