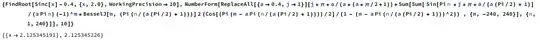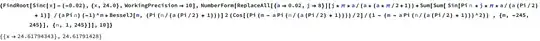$\def\sinc{\operatorname{sinc}} \def\J{\operatorname J}\def\Re{\operatorname{Re}}$Rewriting:
$$\sinc(x)=a\mathop\implies^{x=\frac{\sin(w)}a}\begin{matrix}\sin(w)+aw=(2k+1)\pi a\\\sin(w)-aw=2k\pi a\end{matrix},k\in\Bbb Z$$
lets us invert $\sinc(x)$ via complex Fourier series; Fourier sine series entails a longer
derivation. Unfortunately, the inverse of $\sin(x)-ax;a>0,\left[-\frac\pi2,\frac\pi2\right]$, is not a function close to the endpoints, so inverting it would make slight Fourier series inaccuracies. So, we can find the even $a<0$ roots and odd $a>0$ roots both exactly as well as approximate the odd $a<0$ roots and even $a>0$ roots. Also, Fourier series on smaller intervals than this one gives us the rest of the branches of the inverse function, but the result would be more complicated. Let $f(w)=\sin(w)+aw,\left[-\frac\pi2,\frac\pi2\right]$ and $f^{-1}(w)=g(w),[-L,L]=\left[-f\left(\frac\pi2\right), f\left(\frac\pi2\right)\right]=\left[-\frac{\pi a}2-1,\frac{\pi a}2+1\right]$:
$$\frac{\sin(g(x))}a=\sum_{n\in\Bbb Z}e^\frac{\pi i n x}L \frac1{2L}\int_{-L}^L \frac{\sin(g(t))}a e^{-\frac{\pi i n t}L}dt\mathop=^{t\to g(t)}\Re\sum_{n=1}^\infty e^\frac{\pi i n x}L\int_{-\frac\pi2}^\frac\pi2\frac{\sin(t)}{aL}e^{-\frac{\pi i n}Lf(t)}df(t)$$
Now integrate series coefficients by parts and sum over its constant term:
$$\frac{\sin(g(x))}a=\frac x{aL}-\Re\sum_{n=1}^\infty e^\frac{\pi inx}L\frac i{\pi a n }\int_{-\frac\pi2}^\frac\pi2 \cos(t)e^{-\frac{\pi i n}L f(t)}dt$$
Unfortunately, this integral likely has no closed form, so a Jacobi-Anger expansion suffices:
$$\int_{-\frac\pi2}^\frac\pi2 \cos(t)e^{-\frac{\pi i n}L(\sin(t)+at)}dt=\sum_{m\in\Bbb Z}(-1)^m J_m\left(\frac{\pi n}L\right)\int_{-\frac\pi2}^\frac\pi2\cos(t)e^{\left(m-\frac{\pi a n}L\right)it}dt=-2\sum_{m\in\Bbb Z} J_m\left(\frac{\pi n}L\right)\frac{(-1)^m\cos\left(\frac{\pi v}2\right)}{v^2-1},v=m-\frac{\pi a n}L$$
Expanding $\sum\limits_{m\in\Bbb Z}$ into $\sum_\limits{m=1}^\infty$ complicates the result and $\Re\left(i e^\frac{\pi i n x}L\right)=-\operatorname{Im
}\left(e^\frac{\pi i n x}L\right)=-\sin\left(\frac{\pi n x}L\right)$. $\frac{\sin(g(w))}a$ inverts $w+\sin^{-1}(a w)$ giving $\sinc^{-1}_j(a)=\frac{\sin(g(\pm\pi ja))}a$ which is the $j$th largest solution to $\sinc(x)=a$. Therefore:
$$\bbox[2px,border:solid blue 3px]{\sinc^{-1}_j(x)=\frac{2\pi j}{\pm\pi x+2}+\frac2{\pm\pi x}\sum_{n=1}^\infty\sum_{m\in\Bbb Z}\frac{(-1)^mJ_m\left(\frac{2\pi n}{\pm\pi x+2}\right)\cos\left(\frac\pi2\left(\frac{\pm2\pi n x}{\pm\pi x+2}-m\right)\right)\sin\left(\frac{\pm2\pi^2n j x}{\pm\pi x+2}\right)}{n\left(1-\left(\frac{\pm2\pi n x}{\pm\pi x+2}-m\right)^2\right)},|x|>\frac2\pi}$$
where if $x>0$, then $j=2k+1$ and we choose “$+$” while if $x<0$, then $j=2k$ and we choose “$-$”. Shown here:
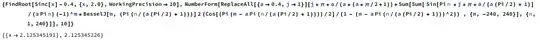
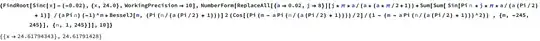
using the Mathematica code:
ReplaceAll[{a->x,j->c}][j*\[Pi]*a/(a*(a*\[Pi]/2+1))+Sum[Sum[ Sin[Pi n *j*\[Pi]*a/(a (Pi/2) + 1)] /(a Pi n) (-1)^m*BesselJ[m, (Pi (n/(a (Pi/2) + 1)))] 2 (Cos[(Pi (m - a Pi (n/(a (Pi/2) + 1))))/2]/(1 - (m - a Pi (n/(a (Pi/2) + 1)))^2)) , {m, -b, b}], {n, 1,b}]]
for given $x,c,b$. Note that Wolfram Cloud states “General::stop: Further output of General::munfl will be suppressed during this calculation” for large $n$, but is still numerically accurate. The series converges more slowly near extrema, but it usually converges a bit more quickly than $\sum_{n=1}^\infty\frac1{n^2}$, like in the above examples. Also, if $x<0$, then $j=2k+1$ and we choose “$+$” or if $x>0$, then $j=2k$ and choose we “$-$”, then the formula gives approximations to the corresponding roots. Lastly, Burniston and Siewert found an integral solution