I am examining the expression $a \cdot \sin(x) =\sin(a \cdot x)$ where $a$ is a rational constant. Is there a way to determine which values of $x$ would be valid? Does it only hold true for certain values of $a$?
-
somebody please explain to me why we cannot simply differentiate both sides twice or why we are not dealing with a function , as @IanMateus said. Thanks. – sigmatau Jul 12 '13 at 02:06
-
2$1=2x.$ Differentiate both sides. Then $0=2.$ Contradiction, therefore there are no solutions to this equation. – Ian Mateus Jul 12 '13 at 02:09
-
@IanMateus Good example. Where is the contradiction coming from?I'm looking for a deeper understanding of the contradiciton.. – sigmatau Jul 12 '13 at 02:13
-
If $a$ is an integer, it's true whenever $x$ is a multiple of $\pi$. – Dan Jul 12 '13 at 02:13
-
@AmireBendjeddou I'm sure there is an old post here on math.SE explaining it much better than me, but roughly it is because $2x$ is constant, it is a number. It is like $\frac{d}{d4}$, makes no sense: differentiation with respect to a number? – Ian Mateus Jul 12 '13 at 02:19
-
ok got it! @IanMateus. – sigmatau Jul 12 '13 at 02:23
-
I doubt there will be a closed-form formula for these curves... http://i.stack.imgur.com/2jlSI.png ($x$ on the $x$-axis, $a$ on the $y$-axis, both between $0$ and $4\pi$) – Jul 12 '13 at 02:52
-
If you have access to a graphing application, I would suggest graphing $y=a\sin,x$ and $y=\sin(ax)$ on the same set of axes: do this, for instance, for $a=-1$, $a=2$, $a=\sqrt2$, $a=5$, and $a=5.5$. Play around a bit! Where the two graphs intersect, you have an occurrence of your relation. – Lubin Jul 12 '13 at 03:17
-
You can get a series solution, like here for about $0.7\le a\le 1.3$ for all branches while solving for $a$ requires the inverse of sinc. However the first expansion has a small convergence region and the second is essentially a restatement of the solution to $\text{sinc}(ax)=b$, so it does not seem worth posting – Тyma Gaidash Nov 30 '23 at 18:40
5 Answers
If $a$ is not $0$, $1$ or $-1$, $\sin(ax)/\sin(x)$ is a non-constant meromorphic function, so there will be at most a discrete set of solutions for $x$. If $a = m/n$ with $m$ and $n$ relatively prime integers, writing $x = nt$ you want to solve $f(t) = n \sin(mt) - m \sin(nt) = 0$. This is periodic with period $2 \pi$, and is $0$ at multiples of $\pi$. The interesting question is whether there are other real solutions. It appears that there always are unless $m$ or $n$ is $1$.
WLOG assume $1 < m < n$. Note that $f(k\pi/n) = n \sin(km\pi/n)$ for integers $k$. The points $x_k = k m\pi/n$ for $k = 0, 1, \ldots, n$ are separated by a distance $< \pi$, and since $x_{n} - x_0 = m \pi \ge 2\pi$ there must be at least one $x_j$ in the interval $(\pi, 2 \pi)$ where $\sin(x_j) < 0$, i.e. $f(x_j/m) < 0$ and at least one $x_k$ in the interval $(0, \pi)$ where $\sin(x_k) > 0$, i.e. $f(x_k/m) > 0$. By the Intermediate Value Theorem, between $x_k/m$ and $x_j/m$ there is some $x$ with $f(x) = 0$.
- 448,999
Not an answer but an observation.
If $(a,x)$ is a solution for the equation: $$a \sin(x) = \sin(ax)$$
then so does $(\pm a,\pm x)$ and $(\pm a^{-1}, \pm ax)$. Ignoring the trivial case $a = 0$ or $\pm 1$ and $x = 0$, we can concentrate on the case where $a > 1$ and $x > 0$. We can rewrite the equation as:
$$\frac{\sin x}{x} = \frac{\sin(ax)}{ax}\quad\quad\text{(assume a > 1)}\tag{*1}$$
Ploting $\frac{\sin x}{x}$ vs $x$, one immediately see that $(*1)$ doesn't have any solution for $|x| <$ some $x_c \sim 2.777068336$. $x_c$ is a root of the equation:
$$\frac{\sin x}{x} = \frac{1}{\sqrt{1+\beta^2}} \sim 0.128374554$$ where $\beta \sim 7.725251837$ itself is a root of another equation $\tan \beta = \beta$.
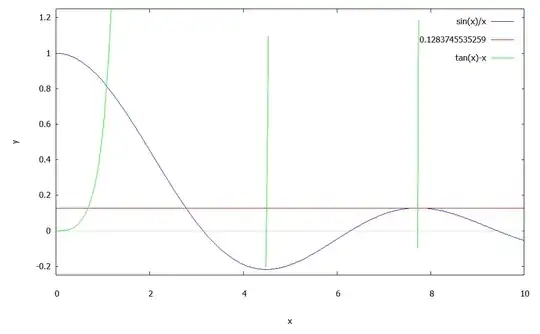
Update
For $a > 0$, rational, express $a$ as a fraction $\frac{m}{n}$ in its lowest term. Let $x = n \theta$ and $d = \max(m,n)$. We can rewrite the equation once again as:
$$\begin{align} & a \sin(x) = \sin(a x)\\ \iff & m \sin(n\theta) - n \sin(m\theta) = 0\\ \iff & \left(m U_{n-1}(\cos\theta) - n U_{m-1}(\cos\theta)\right)\sin\theta = 0 \end{align}$$ where $U_k(t)$ is the Chebyshev's polynomial of the $2^{nd}$ kind. Asides from the trivial solutions:
$$\sin\theta = 0 \iff x = 0, \pm n\pi, \pm 2n\pi, \ldots$$
$ \cos\theta $ will be a root of a polynomial of degree $d-1$: $G_{m,n}(t) = m U_{n-1}(t) - n U_{m-1}(t)$.
Notice $U_k(1) = k+1$, $U_k(-1) = (-1)^k(k+1)$ and in general $U_k(-x) = (-1)^kU_k(x)$. We see
when $m$ and $n$ have same parity, i.e. both of them are odd.
- $G_{m,n}(1) = G_{m,n}(-1) = 0$
- $G_{m,n}(t) = (t^2-1) P_{m,n}(t^2)$ for some polynomial $P_{m,n}(\cdot)$ of degree $\frac{d-3}{2}$.
When $m$ and $n$ have different parity, i.e. one of them is odd, the other is even.
- $G_{m,n}(1) = 0$
- $G_{m,n}(t) = (t-1) Q_{m,n}(t)$ for some polynomial $Q_{m,n}(\cdot)$ of degree $d-2$.
This means when
$$m, n \le \begin{cases}6,& m \not\equiv n \pmod{2}\\11,& m \equiv n \pmod{2}\end{cases}$$
The root $ \cos\theta $ of $G_{m,n}(t)$ can be expressed in terms of radicals.
The simplest example is $\frac{m}{n} = \frac23$, we have:
$$\begin{align} &Q_{2,3}(t) = 8 t + 2 \\ \implies & \cos\theta = t = -\frac14\\ \implies & x = n\theta \stackrel{\text{can be}}{=} \pm3\cos^{-1}(-\frac14) + 6K\pi,\text{ where } K \in \mathbb{Z} \end{align}$$
Another examples is $\frac{m}{n} = \frac35$, we have:
$$\begin{align} &P_{3,5}(t) = 48 t - 8 \\ \implies & \cos\theta = \sqrt{t} = \pm\frac{1}{\sqrt{6}}\\ \implies & x = n\theta \stackrel{\text{can be}}{=} \pm 5\cos^{-1}(\pm\frac{1}{\sqrt{6}}) + 10K\pi,\text{ where } K \in \mathbb{Z}\\ \iff & x = n\theta \stackrel{\text{can be}}{=} \pm 5\cos^{-1}(\frac{1}{\sqrt{6}}) + 5K'\pi,\text{ where } K' \in \mathbb{Z} \end{align}$$
Other non-trivial solutions for small $m,n$ can be derived in similar manner.
- 122,701
If $a = 0, \pm 1$ there are infinitely many solutions. If $a$ is an integer, the solution is $\pi n, n \in \mathbb{Z}$. Otherwise, the solution is $2\pi dn, n \in \mathbb{Z}$, where $d$ is twice the denominator of the fraction.
- 1,682
-
There can be other solutions. For example, if $a = 2/3$ there is a solution $x \approx 1.741291869 \pi$. – Robert Israel Jul 12 '13 at 02:32
-
-
Suppose $\alpha = m/n$ with $m, n$ relatively prime, and $x = n t$. $\sin(\alpha x) = \sin(mt) = P_m(\cos(t)) \sin(t)$ where $P_m$ is a certain polynomial of degree $m-1$, and similarly $\sin(x) = P_n(\cos(t)) \sin(t)$. If $r$ is a root of the polynomial $n P_m(s) - m P_n(s)$ with $-1 \le r \le 1$, take $t$ so $\cos(t) = r$. In general, the roots won't have a "closed form" expression. – Robert Israel Jul 13 '13 at 01:50
-
1$P_m(s)$ above is really $U_{m-1}(s)$, the Chebyshev's polynomial of second kind. For $n,m$ both very small, the root $n U_{m-1}(s) - m U_{n-1}(s)$ can be expressed in terms of radicals. e.g. For the case $a = 2/3$, a solution is $x = 3\cos^{-1}(-\frac14) \sim 1.741291869\pi$. – achille hui Jul 14 '13 at 04:17
There will be no explicit solutions in general for 'a' being Real except those special solutions in the answer above. You need to solve the equation numerically to arbitrary precision for x given 'a' using a computer or by hand if you like Newton's method. Since sine is periodic you will find that it has infinitely many solutions.
- 163
This is not intended to really answer the question, but I think it is appropriate to add as an answer.
An implicit plot of the values for $a$ and $x$ which satisfy the given relation is shown below. Clearly, there are solutions for rational $a$ values, but a closed form solution for $x$ is likely difficult for arbitrary $a$, given the previous answers to this question.
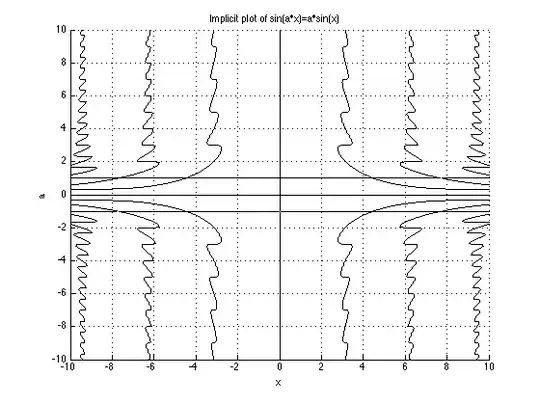
- 5,598