3

How do I prove $(-1)\cdot(-1)=1$ (or in other words that $-1$ is the multiplicative inverse of itself), based only on the field axioms?

Thanks

Elias Costa
  • 14,658
MCL
  • 522

5 Answers5

9

This is to get the result of the multiplication $ \cdot $ of $- 1 $ by $-1$. The number $-1$ is the symmetric of $1$ with respect to addition $ + $. The axioms that relate addition $+$ to multiplication $\cdot$ are distributivity to the left and right distributivity. Any way to prove this result has to pass through the axiom distributive property which connects the multiplication operation with the addition operation. These equality is a relatively easy exercise.

\begin{align} (-1)\cdot (-1)= & (-1)\cdot(-1)+\color{red}{0}\\ = & (-1)\cdot(-1)+\color{red}{[(-1)+1]}\\ = & (-1)(-1)+\color{red}{\Big(1\cdot(-1)+1\cdot 1\Big)}\\ = & \color{blue}{\Big((-1)(-1)+1\cdot(-1)\Big)}+\color{red}{1\cdot 1} \\ = & \color{blue}{\Big([(-1)+1]\cdot(-1)\Big)}+\color{red}{1} \\ = & \color{blue}{\Big(0\cdot(-1)\Big)}+\color{red}{1} \\ = &\color{blue}{0}+ \color{red}{1}\\ =&1 \end{align}

Elias Costa
  • 14,658
5

$\textbf{Hint:}$ Think about $(1-1)(1-1)$.

Arthur
  • 5,524
1

Principles of Mathematical Analysis - Walter Rudin, 3rd Ed, p7:

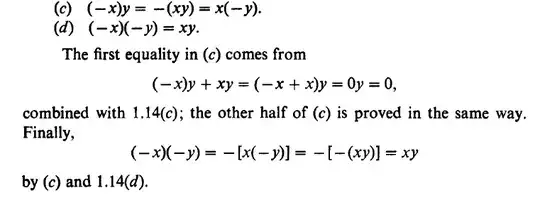
enter image description here

Franck Dernoncourt
  • 1,159
  • Regarding the last equality, -(-(xy))=xy, here is the proof: By addition inverses axiom, -x+x=0. Replace x by -x. This gives -(-(x))=x – Franck Dernoncourt Oct 25 '13 at 15:18
  • By the way you will still have to prove $0 \cdot y = 0$, this shouldn't be difficult though. – Arthur Oct 25 '13 at 15:24
  • Also still need to prove that ax+b=0 has one and only solution but I know how to prove these two, so that's really good enough for me. – MCL Oct 25 '13 at 15:28
1

$(-1) \cdot (-1)=(-1) \cdot (-1)+(-1) \cdot (1)-(-1) \cdot 1=(-1) \cdot (-1+1)-(-1)=1.$

Leox
  • 8,120
0

$-1\cdot\text{sth.}=\text{additive inverse of sth.}$,thus $-1\cdot(-1)=1$, as $1$ is the additive inverse of $-1$.

Michael Hoppe
  • 18,103
  • 3
  • 32
  • 49