How can I find asymptote of this function?

Question

I have been trying this the whole night and couldn't find the answer. This is homework, by the way. $$f(x) = \sqrt{x^2+1}$$

Answer 1

The answer is $g(x) = x$, because $f(x) - g(x)$ goes to zero as $x$ goes to infinity.

Answer 2

Hint: Since $f(x) \to \infty$ as $x \to \infty$, the best we can hope for is an oblique asymptote. Noting that $x^2 + 1 \approx x^2$ for very large $x$, we could guess that $f(x) - x \to 0$ as $x \to \infty$.

To prove this a bit more formally, consider the quantity

$$\sqrt{x^2 + 1} - x = \left(\sqrt{x^2 + 1} - x\right) \frac{\sqrt{x^2 + 1} + x}{\sqrt{x^2 + 1} + x}$$ and see if you can simplify it.

Answer 3

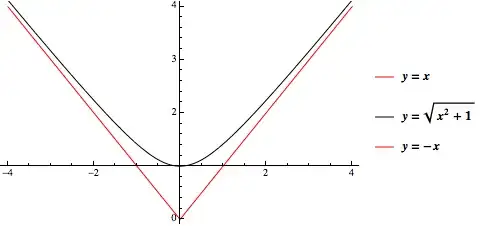
To find an asymptote of a function $y = f(x)$, one needs to evaluate a limits $$ k = \lim_{x \to \infty} \frac yx \\ b = \lim_{x \to \infty} (y - kx) $$ In general, you need to evaluate two pairs of limits when $x \to \pm \infty$, since they might not coincide, which is the case in your problem: \begin{align} k_1 &= \lim_{x \to +\infty} \frac yx = \lim_{x \to +\infty}\frac {\sqrt{x^2+1}}x = \lim_{x \to +\infty} \sqrt{1+\frac 1{x^2}} = 1 \\ k_2 &= \lim_{x \to -\infty} \frac yx = \lim_{x \to -\infty}\frac {\sqrt{x^2+1}}x = \lim_{x \to +\infty}\frac {\sqrt{x^2+1}}{-x} = -\lim_{x \to +\infty} \sqrt{1+\frac 1{x^2}} = -1 \\ b_1 &= \lim_{x \to +\infty} (y - k_1x) = \lim_{x \to +\infty} \sqrt{x^2-1} - x = \lim_{x \to +\infty}\frac {\left ( \sqrt{x^2-1} - x \right )\left( \sqrt{x^2-1} + x\right )}{\sqrt{x^2-1}+x} = \\ &= -\lim_{x \to +\infty} \frac 1{\sqrt{x^2-1}+x} = 0 \\ b_2 &= \left | \text{same analysis} \right | = 0 \end{align} So, your function has two oblique asymptotes when $x \to -\infty$ and $x \to +\infty$ correspondingly: $$ y = \pm x $$

Answer 4

A related problem. Here is how you advance

$$ f(x)=\sqrt{1+x^2}=\sqrt{x^2}\sqrt{1+\frac{1}{x^2}}=|x|\sqrt{1+\frac{1}{x^2}}\sim_{x\to \pm \infty} |x|. $$

Note:

$$ \sqrt{x^2}=|x|. $$