Find the asymptotes of $$ \lim_{x \to \infty}x\cdot\exp\left(\dfrac{2}{x}\right)+1. $$ How is it done?
Asked
Active
Viewed 3,446 times
3 Answers
5
A related problem. We will use the Taylor series of the function $e^t$ at the point $t=0$,
$$ e^t = 1+t+\frac{t^2}{2!}+\frac{t^3}{3!}+\dots .$$
$$ x\,e^{2/x}+1 = x ( 1+\frac{2}{x}+ \frac{1}{2!}\frac{2^2}{x^2}+\dots )+1=x+3+\frac{2^2}{2!}\frac{1}{x}+\frac{2^3}{3!}\frac{1}{x^2}+\dots$$
$$ = x+3+O(1/x).$$
Now, you can see when $x$ goes to infinity, then you have
$$ x\,e^{2/x}+1 \sim x+3 $$
Here is the plot of $x\,e^{2/x}+1$ and the Oblique asymptote $x+3$
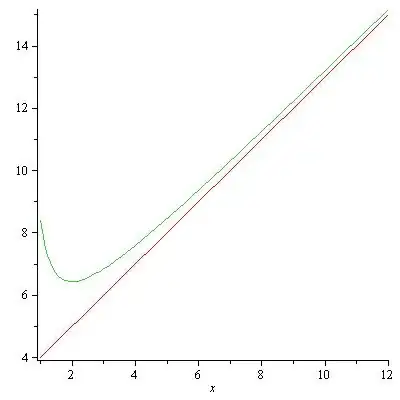
Mhenni Benghorbal
- 47,431
-
Could you further explain the second step? – Nov 28 '12 at 09:42
-
@Grant: Note that he cited that $x+3$ is an Oblique asymptote. – Mikasa Nov 28 '12 at 10:06
-
@Grant: See the edit. – Mhenni Benghorbal Nov 28 '12 at 10:14
-
1@BabakSorouh: Thanks for answering him. – Mhenni Benghorbal Nov 28 '12 at 10:14
-
@Grant: Try to plot the two functions $x,e^{2/x}+1,, x+3$ on the same graph and see what happens when x gets bigger. – Mhenni Benghorbal Nov 28 '12 at 10:17
-
Thank you for your effort, but I still don't understand how can you transform a simple expression ( x*e^(2/x) ) to some kind of series. – Nov 28 '12 at 10:45
-
Aha, Taylor series! Thank you. – Nov 28 '12 at 11:05
-
@Mhenni Why are the first two terms of the taylor series expansion enough to find the asymptote? Certainly there are functions where the first two terms wouldn't suffice to give an accurate approximation. – TheRealFakeNews May 14 '13 at 18:31
1
$$\lim_{x \to \infty}\frac d{dx}\left( x\cdot\exp\left(\dfrac{2}{x}\right)+1\right)=\lim_{x \to \infty}\exp\left(\frac2x\right)-\frac{2\exp\left(\frac2x\right)}{x}=1$$ therefore your function rises like $x$ asymptotically.
draks ...
- 18,449