Some time ago, I asked this here. A restricted form of the second question could be this:
If $f$ is a function with continuous first derivative in $\mathbb{R}$ and such that $$\lim_{x\to \infty} f'(x) =a,$$ with $a\gt 0$, then $$\lim_{x\to\infty}f(x)=\infty.$$
To prove it, I tried this:
There exist $x_0\in \mathbb{R}$ such that for $x\geq x_0$, $$f'(x)\gt \frac{a}{2}.$$ There exist $\delta_0\gt 0$ such that for $x_0\lt x\leq x_0+ \delta_0$ $$\begin{align*}\frac{f(x)-f(x_0)}{x-x_0}-f'(x_0)&\gt -\frac{a}{4}\\ \frac{f(x)-f(x_0)}{x-x_0}&\gt f'(x_0)-\frac{a}{4}\\ &\gt \frac{a}{2}-\frac{a}{4}=\frac{a}{4}\\ f(x)-f(x_0)&\gt \frac{a}{4}(x-x_0)\end{align*}.$$ We can assume that $\delta_0\geq 1$. If $\delta_0 \lt 1$, then $x_0+2-\delta_0\gt x_0$ and then $$f'(x_0+2-\delta_0)\gt \frac{a}{2}.$$ Now, there exist $\delta\gt 0$ such that for $x_0+2-\delta_0\lt x\leq x_0+2-\delta_0+\delta$ $$f(x)-f(x_0+2-\delta_0)\gt \frac{a}{4}(x-(x_0+2-\delta_0))= \frac{a}{4}(x-x_0-(2-\delta_0))\gt \frac{a}{4}(x-x_0).$$ It is clear that $x\in (x_0,x_0+2-\delta_0+\delta]$ and $2-\delta_0+\delta\geq 1$.
Therefore, we can take $x_1=x_0+1$. Then $f'(x_1)\gt a/2$ and then there exist $\delta_1\geq 1$ such that for $x_1\lt x\leq x_1+\delta_1$ $$f(x)-f(x_1)\gt \frac{a}{4}(x-x_1).$$ Take $x_2=x_1+1$ and so on. If $f$ is bounded, $(f(x_n))_{n\in \mathbb{N}}$ is a increasing bounded sequence and therefore it has a convergent subsequence. Thus, this implies that the sequence $(x_n)$: $$x_{n+1}=x_n+1,$$ have a Cauchy's subsequence and that is a contradiction. Therefore $\lim_{x\to \infty} f(x)=\infty$.
I want to know if this is correct, and if there is a simpler way to prove this. Thanks.
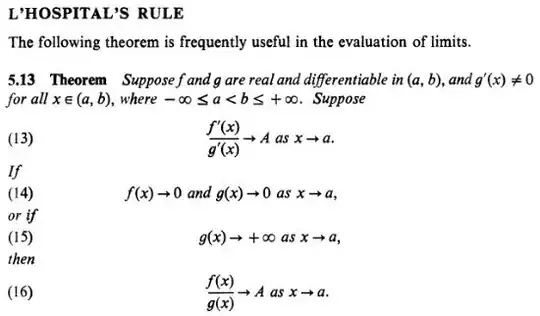
 (Plot of our imaginative function - $f(x)$ vs $x$)
(Plot of our imaginative function - $f(x)$ vs $x$)