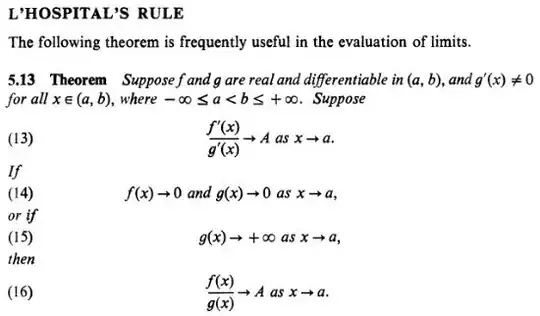2

L.Hopital rule can be used to find the limits of the form

$\lim_{x \to a} \dfrac{f(x)}{g(x)}$ when $\lim_{x \to a}f(x)=\lim_{x \to a}g(x)=\infty$

Today I saw page claiming that $\lim_{x \to a} f(x)=\infty$ is not necessary (When $\lim _{x \to a}g(x)=\infty$) . Is it true? Can it be proved that this condition isn't necessary.

Edit: To clarify, I am solving a limit problem with L.Hopital where $f(x)\neq \infty$[This doesn't prove it, I am trying to clear what I am trying to ask]

$\lim_{x \to \infty}\dfrac{1}{x^2}$ (as $\lim_{x \to \infty} x^2 =\infty$, limit of numerator need not ne $\infty$)

Applying L.Hopital once:

$\implies\dfrac{0}{2x}$ (as $\lim_{x \to \infty}2x=\infty$,limit of numerator need not ne $\infty$)

Applying L.Hopital again:

$\implies \dfrac{0}{2}=0$

Edit: enter image description here

Mathslover
  • 21
  • see user71352 link – DSinghvi Aug 08 '14 at 18:25
  • Yes, the Theorem as stated is true. You can find a proof in baby Rudin (it look like that's where your image is taken from). This question has answers with proofs here as well. See this, e.g.. – David Mitra Aug 08 '14 at 19:28
  • There are a lot of non-answers here stating that this generalization is never useful anyway. But this is not true! If the numerator has a finite limit (while the denominator has an infinite limit), then sure, the limit is zero and this result is not needed. But if you don't know what the limit of the numerator is, or if the numerator is oscillating with no limit (and is not bounded either, since this would also make the limit zero), then this result is useful! An example of its use (where the numerator is mostly unknown) is at https://math.stackexchange.com/questions/51596/#51629 – Toby Bartels Oct 28 '19 at 15:33

3 Answers3

3

I think what you are looking for is the proof found in here using the Cesaro-Stolz Theorem. http://www.imomath.com/index.php?options=686

One of the cases is when $\lim_{x\to a}g(x)=\infty$ but makes no hypothesis on $f$.

Another link that may help you is this one:

In this link a proof is provided that seems to match what your picture wants.

Tom Lynd
  • 1,342
user71352
  • 13,038
0

They can also both have limits of 0. You can prove this by taking the reciprocal of each function and of the entire ratio. The resulting expression is equivalent to the original but now the numerator and denominator approach zero

  • I mean we can still apply L.Hopital even if numerator $\neq \infty$ while denominator $= \infty$ – Mathslover Aug 08 '14 at 18:14
  • Yeah but you have to reduce it to inf/inf or 0/0 somehow, then apply the rule. – dylan7 Aug 08 '14 at 18:35
  • @user163751 Thats precisely what I am asking. Can I apply the rule if its not of the form inf/inf, rather p/inf where p$\neq \infty$ – Mathslover Aug 08 '14 at 18:44
  • Well for what u said the answer is just zero. What you said is not an indeterminate form, so the rule cannot be applied and doesn"t need to be, assuming p is not 0. – dylan7 Aug 08 '14 at 18:47
  • To be more specific the rule is only applied to limits that can't be determined by normal means, but must be in the form 0/0 or inf/inf, hence indeterminate. There are other forms that reduce to these that are called indeterminate too, I.e 1^inf. The one you said is not one of them. – dylan7 Aug 08 '14 at 18:51
  • @user163751 [1]: http://i.stack.imgur.com/IhUhD.jpg – Mathslover Aug 08 '14 at 18:58
-1

if you need to find $\lim_{x\rightarrow a} \frac{f(x)}{g(x)}$ and you have $\lim_{x\rightarrow a} f(x) \neq \infty$ and $\lim_{x\rightarrow a} g(x) = \infty$, then l'hopital's rule doesn't apply: limiting to (something finite)/$\infty$ gives 0, as opposed to something indeterminate.

Even worse, trying to use L'Hopital's rule when it's inappropriate can get you into trouble: $$\lim_{x\rightarrow 0}\frac{\sqrt[3]{x}}{\csc(x)}=\frac{0}{\infty}=0$$ But if you apply l'hopital's rule this gives $$\frac{1}{3}\frac{x^{-\frac{2}{3}}}{\csc x \cot x} = \frac{\infty}{\infty}$$ and repeated applications of the rule don't get rid of this indeterminate form.

Dan Uznanski
  • 11,025
  • Can you prove that L.Hopital can't be applied in the given case?? – Mathslover Aug 08 '14 at 18:32
  • It's not so much that it can't be applied -- you'd still get 0 -- but that there's no point. L'Hopital's Rule is specifically for the situation where a simple application of limit rules leaves you with an indeterminate situation. This isn't indeterminate. – Dan Uznanski Aug 08 '14 at 18:39
  • I am trying to ask if L.Hopital can be applied in the case where numerator $\neq \infty$ as $x$ goes to $a$? And yes its not indeterminate form but I am working on a problem which simplifies if I assume so – Mathslover Aug 08 '14 at 18:42
  • It can't generally. Consider (5x+2)/sin(x) as x approaches 0. This gives 2/0 --> $\infty$; applying l'hopital gives 5/1 ---> 5 and that's wrong. – Dan Uznanski Aug 08 '14 at 18:49
  • But $\lim_{x \to 0} \sin x \neq \infty$, the denomenator is required to be infinity – Mathslover Aug 08 '14 at 18:50
  • Oh fine. $\sqrt[3]x/csc(x)$ as x approaches 0. Without l'hopital, this is $0/\infty$; applying l'hopital you get $\infty/\infty$ and that never goes away no matter how far you go. – Dan Uznanski Aug 08 '14 at 18:54
  • It doesn't prove anything unless you simplify inf/inf to something non zero – Mathslover Aug 08 '14 at 19:01
  • That example doesn't invalidate LHR for the case of $\text{something}/\infty$. LHR states that if the limit of the denominator $g$ is $\infty$ AND limit of the quotient of derivatives $f'/g'$ exists AND $f'$ and $g'$ are continuously differentiable around the point the limits are taken, then $\lim f/g=\lim f'/g'$. – Mark Viola Nov 29 '18 at 00:00
  • This answer is wrong, because the rule also works when the numerator is arbitrary and the denominator is infinite, which is exactly what the OP was asking about. (Proofs are in the links in the answer by user71352.) In particular, the limit of the expression with $\csc x\cot x$ is zero, and so the rule is valid (despite not being useful in this case). – Toby Bartels Oct 28 '19 at 15:52
  • @MarkViola : Incidentally, $f$ and $g$ don't have to be continuously differentiable (and $f'$ and $g'$ don't have to be differentiable at all, but that was probably just a typo). Sometimes this is assumed in Calculus textbooks to simplify the proof (especially if they never state Bezout's Theorem), but it's enough that $f$ and $g$ are differentiable (and $g' \ne 0$), in other words that $f'/g'$ is defined in the direction of the limit. (See the proofs at the links in the answer by user71352, which never use continuity of the derivatives.) – Toby Bartels Oct 28 '19 at 15:56
  • @TobyBartels Yes, that was indeed a typo. – Mark Viola Oct 28 '19 at 16:28