2

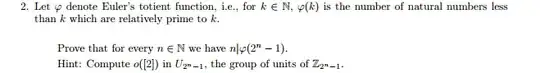
enter image description here

Let $\varphi$ denote Euler's totient function, i.e., for $k\in\mathbb N$, $\varphi(k)$ is the number of natural numbers less tan $k$ which are relatively prime to $k$.

Prove that for every $n\in\mathbb N$ we have $n\mid \varphi(2^n-1)$.
Hint: Compute $o([2])$ in $U_{2^n-1}$, the group of units of $\mathbb Z_{2^n-1}$.

I am totally stuck here for this question. how do I compute o([2])??

any tips or suggestions would be great!

Martin Sleziak
  • 53,687
Dafty
  • 509
  • 3
    Are you aware that if $(a,m) = 1$ then the order of $a$ (mod $m$) divides $\phi(m)$ ? Using Mr. Tamaroff's advice, deduce that the order of 2 (mod $2^n-1$) is $n$ and since $(2,2^n-1) = 1$ ($2^n-1$ is odd), you will get the result. – Amateur Oct 04 '13 at 04:53
  • If you understand Pedro's Hint, you could add a full answer to your question. – robjohn Oct 04 '13 at 07:56

1 Answers1

2

Note that trivially $$2^n\equiv 1\mod 2^{n}-1$$

Now suppose $k<n$. Then $2^k-1<2^n-1$, so...?

Pedro
  • 122,002
  • could you give me an actual example of numbers? I aam having hard time understanding this concept :/ – Dafty Oct 04 '13 at 04:50