How do I integrate $\sec(x)$?

Question

My HW asks me to integrate $\sin(x)$, $\cos(x)$, $\tan(x)$, but when I get to $\sec(x)$, I'm stuck.

Answer 1

Hint: I'm assuming you know the derivatives of $\sec(x)$ and $\tan(x)$.

Since $\frac d{dx}\tan(x)=\sec^2(x)$ and $\frac d{dx}\sec(x)=\sec(x)\tan(x)$,

therefore $\frac d{dx}[\tan(x)+\sec(x)]=\sec(x)[\tan(x)+\sec(x)]$

Note that here: $\sec(x)=\dfrac{\frac d{dx}[\tan(x)+\sec(x)]}{\tan(x)+\sec(x)}$

Now let $u=\tan(x)+\sec(x)$, you get $\sec(x)=\dfrac{du}u$, then you integrate both sides:

\begin{align*}\therefore \int\sec(x)\ dx&=\int\frac{du}u\\\\&=\ln|u|+C\\\\&=\ln|\tan(x)+\sec(x)|+C\end{align*}

Answer 2

$$\int \frac{1}{\cos x} dx =\int \frac{\cos x}{\cos^2 x} dx =\int \frac{d(\sin x)}{1-\sin^2 x}$$ $$=\frac {1}{2}\int (\frac {1}{1-\sin x}+\frac {1}{1+\sin x}) d(\sin x) =\frac {1}{2}\int \frac {d(\sin x)}{1-\sin x}+\frac {1}{2}\int \frac {d(\sin x)}{1+\sin x} $$ $$= -\frac {1}{2}\ln |1-\sin x|+\frac {1}{2}\ln |1+\sin x|+C$$ $$=\frac {1}{2}\ln|\frac {1+\sin x}{1-\sin x}|+C=\frac {1}{2}\ln|\frac {(1+\sin x)^2}{\cos^2 x}|+C$$ $$=\ln|\sec x+\tan x|+C$$ Hope it can help you

Answer 3

$$\int \sec x dx$$

Using Weierstrass substitution,

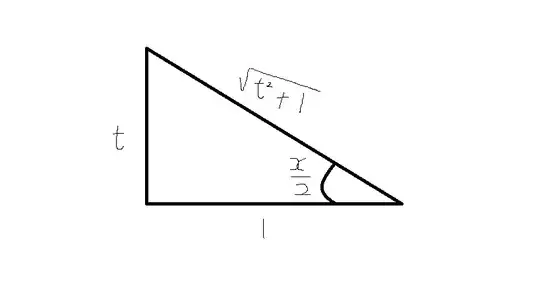
$$\tan x=\tan(\frac{x}{2}+\frac{x}{2}) \iff \tan(\frac{x}{2}+\frac{x}{2})=\frac{2\tan\frac{x}{2}}{1-\tan^2(\frac{x}{2})}$$

$$ \tan(\frac{x}{2}+\frac{x}{2})=\frac{2\tan\frac{x}{2}}{1-\tan^2(\frac{x}{2})}\iff \tan x= \frac{2t}{1-t^2}$$

$$\tan(\frac{x}{2})=t \iff \frac{1}{2}\sec^2(\frac{x}{2})dx=dt$$

$$\frac{1}{2}\sec^2(\frac{x}{2})dx=dt \iff dx= 2\cos^2\frac{x}{2}dt$$

$$dx= 2\cos^2\frac{x}{2}dt \iff dx=\frac{2}{(1+t^2)}dt$$

$$\cos(x)=\cos(\frac{x}{2}+\frac{x}{2}) \iff \cos( \frac{x}{2}+ \frac{x}{2})= \cos^2(\frac{x}{2})-\sin^2(\frac{x}{2})$$

$$\cos^2(\frac{x}{2})-\sin^2(\frac{x}{2})=\frac{1}{t^2+1}-\frac{t^2}{t^2+1} \iff \frac{1-t^2}{t^2+1}=\cos x$$

$$\frac{1-t^2}{t^2+1}=\cos x \iff \sec x=\frac{1+t^2}{1-t^2} $$

$$\int \sec x dx=\int \frac{1+t^2}{1-t^2}. \frac{2}{(1+t^2)}dt \iff \int \frac{1+t^2}{1-t^2}. \frac{2}{(1+t^2)}dt=\int \frac{2}{1-t^2}dt$$

Partial fractions!

$$\frac{2}{1-t^2}\equiv \frac{A}{1-t}+\frac{B}{1+t}\iff 2\equiv A(1+t)+B(1-t)$$

Solution is $t=1, A=1,t=-1,B=1$

$$\int \frac{1}{1+t}+\frac{1}{1-t}dt=\ln|1+t|-\ln|1-t|+c \iff \ln|\frac{1+t}{1-t}|.\ln|\frac{1+t}{1+t}|+c=\ln|\frac{(1+t)^2}{1-t^2}|+c$$

$$\ln|\frac{(1+t)^2}{1-t^2}|+c=\ln|\frac{t^2+2t+1}{1-t^2}|+c \iff \ln|\frac{1+t^2}{1-t^2}+\frac{2t}{1-t^2}|$$

So,

$$\ln|\frac{1+t^2}{1-t^2}+\frac{2t}{1-t^2}| \iff \ln|\sec x + \tan x|$$

This is a standard integral for $\sec x$

Conclusion!

$$\int \sec xdx=\ln|\sec x+\tan x|+c$$

Answer 4

This is p. 361, Chapter 18, Question 12, of Spivak's Calculus (1994 3 edn). I don't know the question number in Calculus (2008 4 edn).

The answers can be found in the Combined Answer Book For Calculus Third and Fourth Editions (2008) by Michael Spivak.

Wikipedia has two solutions too (already overhead), and history on them.