1

I want to prove that $\mathbb N\times \mathbb N$ is countable set using cantor first diagonal method: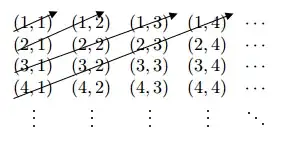

where every-time we count the elemnts on the digonal with the direction of the arrow ($(1,1)\mapsto1,(2,1)\mapsto 2,(1,2)\mapsto3,(3,1)\mapsto4$ etc). I know that if I had same problem with $\mathbb N \cup{0}\times \mathbb N \cup{0}$ I could define cantor's function by $f(x,y)=\frac {(x+y+1)(x+y)}{2}+y$ which I'm not sure its' bijective. How can I define a function according to my scheme?

EDIT: The question is NOT about proving $\mathbb N\times \mathbb N$ is countable but on writing appropriate bijective function for the described diagonal method.

Community
  • 1
  • Look at http://math.stackexchange.com/questions/278679/does-anyone-know-a-closed-form-expression-for-a-bijection-between-mathbbnk/278692#278692. – copper.hat Sep 11 '13 at 07:47
  • Can you not compose the function you know for $\mathbb N \cup{0}\times \mathbb N \cup{0}$ with a bijection from $\mathbb N$ to $\mathbb N \cup{0}$? – Peter Taylor Sep 11 '13 at 08:33
  • To be more specific than copper.hat, see this answer to the linked question (incidentally by copper.hat). $\beta^{-1}$ is the function you seek. – Lord_Farin Sep 11 '13 at 09:10

1 Answers1

0

Hint: Say $X$ and $Y$ are countable, then consider $f : X \times Y \to \mathbb{N}$ be given by

$$f(x,y) = 2^x3^y $$

Prove this is injective.

ILoveMath
  • 10,694