Deriving the rest of trigonometric identities from the formulas for $\sin(A+B)$, $\sin(A-B)$, $\cos(A+B)$, and $\cos (A-B)$

Question

I am trying to study for a test and the teacher suggest we memorize $\sin(A+B)$, $\sin(A-B)$, $\cos(A+B)$, $\cos (A-B)$, and then be able to derive the rest out of those. I have no idea how to get any of the other ones out of these, it seems almost impossible. I know the $\sin^2\theta + \cos^2\theta = 1$ stuff pretty well though. For example just knowing the above how do I express $\cot(2a)$ in terms of $\cot a$? That is one of my problems and I seem to get stuck half way through.

Answer 1

Since $\displaystyle\cot(2a) = \frac{\cos(2a)}{\sin(2a)}$, you would have (assuming you know the addition formulas for sines and cosines): $$\begin{align*} \cos(2a) &= \cos(a+a) = \cos(a)\cos(a) - \sin(a)\sin(a)\\ &= \cos^2(a) - \sin^2(a);\\ \sin(2a) &= \sin(a+a) = \sin(a)\cos(a) + \cos(a)\sin(a)\\ &= 2\sin(a)\cos(a), \end{align*}$$ and therefore $$\begin{align*} \cot(2a) &= \frac{\cos(2a)}{\sin(2a)} = \frac{\cos^2(a) - \sin^2(a)}{2\sin(a)\cos(a)}\\ &= \frac{1}{2}\left(\frac{\cos^2(a)}{\sin(a)\cos(a)}\right) - \frac{1}{2}\left(\frac{\sin^2(a)}{\sin(a)\cos(a)}\right)\\ &= \frac{1}{2}\left(\frac{\cos(a)}{\sin(a)} - \frac{\sin(a)}{\cos(a)}\right)\\ &= \frac{1}{2}\left(\cot(a) - \tan(a)\right)\\ &= \frac{1}{2}\left(\cot(a) - \frac{1}{\cot(a)}\right)\\ &= \frac{1}{2}\left(\frac{\cot^2(a)}{\cot(a)} - \frac{1}{\cot(a)}\right)\\ &= \frac{1}{2}\left(\frac{\cot^2(a) - 1}{\cot (a)}\right). \end{align*}$$

P.S. Now, as it happens, I don't know the formulas for double angles, nor most identities involving tangents, cotangents, etc. I never bothered to memorize them. What I know are:

1. The definitions of tangent, cotangent, secant, and cosecant in terms of sine and cosine;
2. That sine is odd ($\sin(-x) = -\sin(x)$) and cosine is even ($\cos(-x)=\cos(x)$);
3. The addition formulas for sine and cosine;
4. The values of sine and cosine at $0^{\circ}$, $30^{\circ}$, $45^{\circ}$, $60^{\circ}$, and $90^{\circ}$.

(I can derive $\sin^2\theta + \cos^2\theta = 1$ from the above, but in all honesty that one comes up so often that I do know it as well). I do not know the addition or double angle formulas for tangents nor cotangents, so the above derivation was done precisely "on the fly", as I was typing. I briefly thought that I might need to $\cos(2a)$ with one of the following equivalent formulas: $$\cos^2(a)-\sin^2(a) = \cos^2(a) + \sin^2(a) - 2\sin^2(a) = 1 - 2\sin^2(a)$$ or $$\cos^2(a) - \sin^2(a) = 2\cos^2(a) - \cos^2(a) - \sin^2(a) = 2\cos^2(a) - 1,$$ if the first attempt had not immediately led to a formula for $\cot(2a)$ that involved only $\cot(a)$ and $\tan(a) = \frac{1}{\cot(a)}$.

Answer 2

Three examples of algebraic derivations of trigonometric identities as an application of the addition and subtraction formulas.

1. Example on how to deduce the logarithmic transformation formulas (sum to product formulas) from

$$\sin (a+b)=\sin a\cos b+\sin b\cos a,\qquad (1)$$

$$\sin (a-b)=\sin a\cos b-\sin b\cos a.\qquad (2)$$

If you write

$$\left\{ \begin{array}{c} a=\frac{p+q}{2}, \\ b=\frac{p-q}{2},\end{array}\right. \Leftrightarrow \left\{ \begin{array}{c} a+b=p, \\ a-b=q,\end{array}% \right. $$

you get

$$\sin (a+b)+\sin (a-b)=2\sin a\cos b,$$

$$\sin (a+b)-\sin (a-b)=2\sin b\cos a,$$

and thus

$$\sin p+\sin q=2\sin \frac{p+q}{2}\cos \frac{p-q}{2},\qquad (3)$$

$$\sin p-\sin q=2\sin \frac{p-q}{2}\cos \frac{p+q}{2}.\qquad (4)$$

You can use $(3)$ to solve the equation

$$\sin (5x)+\sin x=\sin (3x)$$

that appeared in my exam in 1968. (See a comment of mine to this post ).

2. As for the example in your question we present the following derivation. From

$$\sin (a+b)=\sin a\cos b+\sin b\cos a,\qquad (5)$$

$$\cos (a+b)=\cos a\cos b-\sin a\sin b,\qquad (6)$$

we get

$$\cot (a+b)=\frac{\cos (a+b)}{\sin (a+b)}=\frac{\cos a\cos b-\sin a\sin b}{\sin a\cos b+\sin b\cos a},$$

or dividing the numerator and denominator by $\sin a\cos b$

$$\begin{eqnarray*} \cot (a+b) &=&\dfrac{\dfrac{\cos a\cos b-\sin a\sin b}{\sin a\cos b}}{\dfrac{% \sin a\cos b+\sin b\cos a}{\sin a\cos b}}=\dfrac{\dfrac{\cos a\cos b}{\sin a\cos b}-\dfrac{\sin a\sin b}{\sin a\cos b}}{\dfrac{\sin a\cos b}{\sin a\cos b}% +\dfrac{\sin b\cos a}{\sin a\cos b}} \\ &=&\dfrac{\dfrac{\cos a}{\sin a}-\dfrac{\sin b}{\cos b}}{1+\dfrac{\sin b\cos a}{% \sin a\cos b}}=\dfrac{\cot a-\tan b}{1+\tan b\cot a}=\dfrac{\cot a-\dfrac{1}{% \cot b}}{1+\dfrac{\cot a}{\cot b}} \\ &=&\dfrac{\dfrac{\cot a\cot b-1}{\cot b}}{\dfrac{\cot b+\cot a}{\cot b}}=\dfrac{% \cot a\cot b-1}{\cot b+\cot a},\qquad (7) \end{eqnarray*}$$

a particular case of which (for $a=b$) is given by

$$\cot (2a)=\dfrac{\cot ^{2}a-1}{2\cot a}.\qquad (8)$$

3. The summation and subtraction formula for the tangent. From

$$\sin (a\pm b)=\sin a\sin b\pm \sin b\cos a$$

we get

$$\tan a\pm \tan b=\frac{\sin a}{\cos a}\pm \dfrac{\sin b}{\cos b}=\frac{\sin a\cos b\pm \sin b\cos a}{\cos a\cos b}=\frac{\sin (a\pm b)}{\cos a\cos b}.\qquad (9)$$

Answer 3

If you understand complex numbers there is a very nice mnemonic. We know that $$e^{it} = \cos(t) + i\sin(t).$$

Take real and imaginary parts on the identity $$e^{i(A + B)} = e^{iA}e^{iB} = (\cos(A) + i\sin(A))(\cos(B) + i\sin(B)).$$

Disassemble and the the sum formulae for $\sin$ and $\cos$. To get the differences, use the assignment $B\leftarrow -B$ and the fact that $\cos(-B) = \cos(B)$ and $\sin(-B) = -\sin(B)$.

Answer 4

Maybe this will help? cot(x) = cosx / sinx -> cot(2a) = cos(a + a) / sin(a + a) and then I assume you know these two.

Edit: Had it saved as a tab and didnt see the posted answer, but I still think it would have been best to let you compute the rest by yourself so that you could learn it by doing instead of reading.

Answer 5

I'm not certain, but I think perhaps you need to revisit the basic trigonometric definitions. $$\begin{array}{lll} \sin\theta = \frac{opposite}{hypotenuse}&\csc\theta=\frac{hypotenuse}{opposite}\\ \cos\theta = \frac{adjacent}{hypotenuse}&\sec\theta=\frac{hypotenuse}{adjacent}\\ \tan\theta = \frac{opposite}{adjacent}&\cot\theta=\frac{adjacent}{opposite} \end{array}$$

Having done that, we can now manipulate the definitions. For example

$$\cot\theta = \frac{adjacent}{opposite}\cdot\frac{\frac{1}{hypotemnuse}}{\frac{1}{hypotemnuse}}=\frac{\frac{adjacent}{hypotenuse}}{\frac{opposite}{hypotenuse}}=\frac{\cos\theta}{\sin\theta}$$

or alternatively

$$\cot\theta = \frac{adjacent}{opposite}=\frac{\frac{1}{opposite}}{\frac{1}{adjacent}}=\frac{\frac{1}{opposite}}{\frac{1}{adjacent}}\cdot\frac{hypotenuse}{hypotenuse}=\frac{\frac{hypotenuse}{opposite}}{\frac{hypotenuse}{adjacent}}=\frac{\csc\theta}{\sec\theta}$$

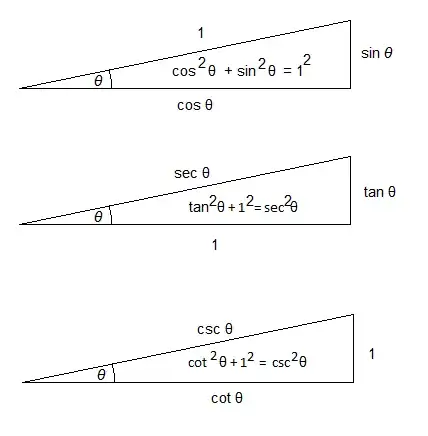
After that, move on to making 3 triangles that are similar to the adjacent-opposite-hypotenuse triangle. These triangles will rotate which side is equal to 1. This is where we get the familiar Pythagorean identities.

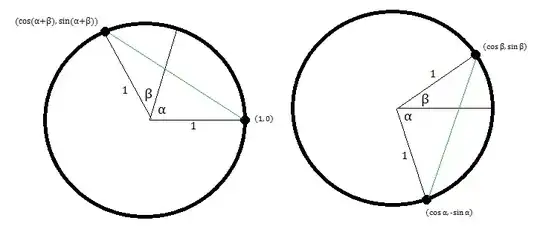
The next step is to derive $\cos (\alpha+\beta)$ and $\sin (\alpha+\beta)$ by setting the lengths (I would use the squares of the lengths though) of the green lines in the diagram equal to each other. It's easy to do, since the endpoints are well known.

Finally, lets derive $\cot(A+B)$ $$\begin{array}{lll} \cot(A+B)&=&\frac{\sin(A+B)}{\cos(A+B)}\\ &=&\frac{\sin A\cos B + \cos A\sin B}{\cos A\cos B - \sin A\sin B}\\ &=&\frac{\frac{\sin A\cos B + \cos A\sin B}{\sin A\sin B}}{\frac{\cos A\cos B - \sin A\sin B}{\sin A\sin B}}\\ &=&\frac{\frac{\cos B}{\sin B}+\frac{\cos A}{\sin A}}{\frac{\cos A\cos B}{\sin A\sin B}-1}\\ &=&\frac{\cot B+\cot A}{\cot A\cot B-1} \end{array}$$ Note that $\cot 2A$ is just $\cot(A+B)$ where $A=B$, so $$\cot 2A = \cot(A+A)=\frac{\cot A+\cot A}{\cot A\cot A-1}=\frac{2\cot A}{\cot^2 A-1}$$ Of course this list isn't comprehensive, for example we didn't derive the sine and cosines laws, nor did we consider the double angle and half angle formulas. But I hope that what little I did present here was helpful.