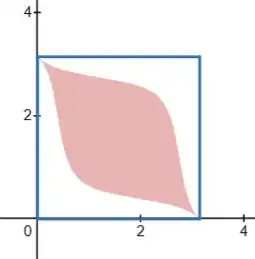
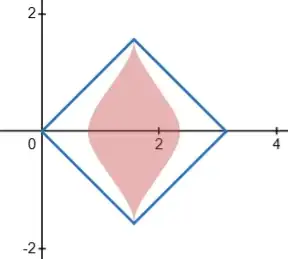
The vertices of a triangle are three unifomly random points on a unit circle. The side lengths are, in random order, $a,b,c$.
Show that $P(ab>c)=\frac12$.
The result is strongly suggested by simulations, and by my attempt shown below.
The simplicity of the result suggests that there may be an intuitive explanation. I am hoping for an intuitive explanation, but if that's not possible then any answer is welcome. (Examples of intuitive explanations are here and here.)
My attempt
Assume that the circle is centred at the origin, and the vertices of the triangle are:
$A(\cos(-2Y),\sin(-2Y))$ where $0\le Y\le\pi$
$B(\cos(2X),\sin(2X))$ where $0\le X\le\pi$
$C(1,0)$
Let:
$a=BC=2\sin X$
$b=AC=2\sin Y$
$c=AB=\left|2\sin\left(\frac{2\pi-2X-2Y}{2}\right)\right|=|2\sin(X+Y)|$
$P\left[ab>c\right]=P\left[2(\sin X)(\sin Y)>|\sin(X+Y)|\right]$
This probability is the ratio of the area of the shaded region to the area of the square in the graph below.
Rotate these regions $45^\circ$ clockwise about the origin, then shrink by factor $\frac{1}{\sqrt2}$, by letting $X=x-y$ and $Y=x+y$.
Using symmetry, we only need to consider the left half of the blue "diamond". Note that in the left half, $0<x<\pi/2$, so $|\sin(2x)|=\sin(2x)$.
$P\left[2(\sin X)(\sin Y)>|\sin(X+Y)|\right]$
$=P\left[2(\sin (x-y))(\sin (x+y))>\sin(2x)\right]$
$=P\left[(\sin^2x)(\cos^2y)-(\cos^2 x)(\sin^2 y)>(\cos x)(\sin x)\right]$
$=P\left[(\sin^2x)(\cos^2y)-(\cos^2 x)(1-\cos^2 y)>(\cos x)(\sin x)\right]$
$=P\left[\cos^2 y>\cos^2 x+(\cos x)(\sin x)\right]$
$=P\left[ -f(x)<y<f(x)\right]$
where $\color{red}{f(x)=\arccos\left((\cos x)\sqrt{1+\tan x}\right)}$.
Noting that $f\left(\frac{\pi}{4}\right)=0$, the probability is
$$\dfrac{\int_{\pi/4}^{\pi/2}f(x)\mathrm dx}{\frac12\left(\frac{\pi}{2}\right)^2}$$
Numerical evidence suggests that $\int_{\pi/4}^{\pi/2}f(x)\mathrm dx=\frac{\pi^2}{16}$, but I don't know how to prove this.
If that's true, then the probability is indeed $1/2$.
Context
This question was inspired by a question, "If $(a,b,c)$ are the sides of a triangle, what is the probability that $ac>b^2$?"
Edit
I found a generalization, which may or may not help in finding an intuitive explanation.
For $k\in\mathbb{R^+}$, we have
$$P(ab<kc)=\frac{2}{\pi}\arctan k$$
or equivalently,
$$P\left(\frac{ab}{c}<k\right)=\frac{\arctan k}{\frac{\pi}{2}}$$
This can be proved using the method in "My attempt" above, which gives
$$P(ab>kc)=\dfrac{\int_{\arctan k}^{\pi/2}\arccos\left((\cos x)\sqrt{1+k\tan x}\right)\mathrm dx}{\frac12\left(\frac{\pi}{2}\right)^2}$$
The integral in the numerator can be evaluated, using the method in @Zacky's answer, as $\frac{\pi}{4}\arctan\frac1k$. So $P(ab<kc)=1-P(ab>kc)=1-\frac{2}{\pi}\arctan\frac1k=\frac{2}{\pi}\arctan k$.