Determine the ellipse tangent to the $x$ and $y$ axes at known points and also tangent to a given line at a unknown point

Question

I'd like to determine the ellipse that is tangent to the $x$ axis at $\mathbf{r_1} = (a, 0), a \gt 0$ and the $y$ axis at $\mathbf{r_2} = (0, b), b \gt 0$, and also tangent to the line $\mathbf{n}\cdot (\mathbf{r} - \mathbf{r_0}) = 0 $ at an unknown point $\mathbf{r_3}$, where $\mathbf{r} = [x, y]^T$ and $\mathbf{n}$ and $\mathbf{r_0}$ are given 2-vectors. This is the task.

My attempt:

The equation of the ellipse is

$ (\mathbf{r - C})^T Q (\mathbf{r - C}) = 1 $

where $\mathbf{C}=[C_x, C_y]^T$ is the unknown center, and $Q$ is $2 \times 2$ symmetric and positive definite, also unknown. That makes a total of $5$ unknowns.

The gradient of the above function of $\mathbf{r}$ is

$ g = 2 Q (\mathbf{r - C}) $

At $\mathbf{r_1}$ the gradient is pointing along the negative $\mathbb{j}$ direction, so that

$ Q ( \mathbf{r_1 - C}) = - k \ \mathbf{j} , k \gt 0$

It follows that

$ \mathbf{r_1 - C} = - k Q^{-1} \mathbf{j} \tag{1}$

Substituting this into the ellipse equation yields

$ k = \dfrac{1}{\sqrt{ \mathbf{j}^T Q^{-1} \mathbf{j} }} $

Now premultiplying $(1)$ by $ \mathbf{j}^T $ gives

$ \mathbf{j}^T ( \mathbf{r_1 - C}) = - C_y = - \sqrt{ \mathbf{j}^T Q^{-1} \mathbf{j} } $

So that

$ C_y = \sqrt{ \mathbf{j}^T Q^{-1} \mathbf{j} } \tag{2} $

Similarly,

$ C_x = \sqrt{ \mathbf{i}^T Q^{-1} \mathbf{i} } \tag{3} $

Now pre-multiplying $(1)$ by $\mathbf{i}^T$ yields

$ C_x - a = \dfrac{\mathbf{i}^T Q^{-1} \mathbf{j}}{\sqrt{ \mathbf{j}^T Q^{-1} \mathbf{j}}} \tag{4}$

So that

$ C_x C_y - a C_y = \mathbf{i}^T Q^{-1} \mathbf{j} \tag{5}$

and similarly,

$ C_y - b = \dfrac{ \mathbf{j}^T Q^{-1} \mathbf{i} } { \sqrt{ \mathbf{i}^T Q^{-1} \mathbf{i}}} \tag{6} $

so that

$ C_x C_y - b C_x = \mathbf{j}^T Q^{-1} \mathbf{i} \tag{7}$

Hence,

$ \dfrac{C_x} { C_y } = \dfrac{a}{b} \tag{8}$

Now if let

$ P = Q^{-1} = \begin{bmatrix} P_{11} && P_{12} \\ P_{12} && P_{22} \end{bmatrix} \tag{9}$

Then using equations $(2),(3),(8)$, we have,

$ b^2 P_{11} = a^2 P_{22} = t^2 \tag{10}$

Now,

$ P_{12} = \sqrt{P_{11} P_{22}} - b \sqrt{P_{11}} = \dfrac{t^2}{ab} - t \tag{11}$

Now considering the given tangent line:

At $\mathbf{r_3}$ which is unknown,

$ (r_3 - C) = - k P \mathbf{n} $ (remember, $P = Q^{-1} $ )

where it is assumed that $\mathbf{n}$ has positive $x$ and $y$ components.

Again, we get $ k = \dfrac{1}{\sqrt{ \mathbf{n}^T P \mathbf{n} } } $

Now, the equation of the line is $\mathbf{n}^T (r - \mathbf{r_0}) = 0 $, so

$ \mathbf{n}^T (\mathbf{r_3 - C}) = \mathbf{n}^T ( \mathbf{r_3} - \mathbf{r_0} + \mathbf{r_0} - \mathbf{C} ) = - \sqrt{ \mathbf{n}^T P \mathbf{n}} \tag{12}$

If we take $\mathbf{n} = [n_1, n_2]^T $ then this equation becomes,

$ n_1 ( r_{0x} - C_x ) + n_2 ( r_{0y} - C_y) = - \sqrt{ P_{11} n_1^2 + P_{22} n_2^2 + 2 P_{12} n_1 n_2 } \tag{13} $

If we define the constant $\alpha = \mathbf{n}^T \mathbf{r_0} $, then $(12)$ becomes

$ \left( (\dfrac{n_1}{b} + \dfrac{n_2}{a} ) t - \alpha \right)^2 = \dfrac{ n_1^2 t^2}{b^2} + \dfrac{n_2^2 t^2}{a^2} + 2 n_1 n_2 \left( \dfrac{t^2}{ab} - t \right) \tag{14} $

which simplifies to

$ - 2 \alpha (\dfrac{n_1}{b} + \dfrac{n_2}{a} ) t + \alpha^2 = - 2 n_1 n_2 t \tag{15}$

Multiplying through by $a b $ gives

$ - 2 \alpha ( a n_1 + b n_2 ) + \alpha^2 a b = - 2 n_1 n_2 a b t \tag{16}$

From which,

$ t = \dfrac{a b \alpha^2 } {2 \left( \alpha (an_1 + bn_2) - n_1 n_2 a b \right) } \tag{17}$

Having obtained $t$, all the parameters of the ellipse can now be computed directly.

I've written a small piece of code to test the above formula for $t$, and found that it is correct.

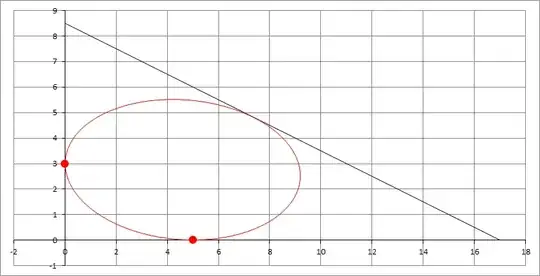
Here's an example with $a= 5, b = 3$, $\mathbf{n }= [1, 2]^T , \mathbf{r_0 } = [5, 6]^T $

Thank you all.

Answer 1

Using coordinate geometry

• An ellipse touches the axes at $(\lambda a,0)$, $(0,\mu b)$ and the line $\dfrac{x}{a}+\dfrac{y}{b}=1$

$$ \left( \frac{x}{\lambda a}+\frac{y}{\mu b}-1 \right)^2=\frac{4xy}{ab} \left( \frac{1}{\lambda}-1 \right) \left( \frac{1}{\mu}-1 \right)$$

• Third contact

$$\frac{1}{\lambda+\mu-2\lambda \mu} \begin{pmatrix} \lambda (1-\mu) a \\ \mu(1-\lambda) b \end{pmatrix}$$

• Brianchon point

$$\frac{1}{1-\lambda \mu} \begin{pmatrix} \lambda (1-\mu) a \\ \mu(1-\lambda) b \end{pmatrix}$$

• Please also refer to older posts of mine here and here.

Answer 2

To find the ellipse tangent to $y=0$ at $(5,0),$ tangent to $x=0$ at $(0,3)$ and tangent to $(x-5)+2(y-6)=0$ or $-\frac1{17}x-\frac2{17}y+1=0,$ we set up five equations in essentially five unknowns by substituting the points in the general equation $$ax^2+bxy+cy^2+dx+ey+f=0,$$ substituting the points and slopes there ($x=0,y=3,dx=0$ and $x=5,y=0,dy=0$) in $$(2ax+by+d)dx+(2cy+e+bx)dy=0,$$ and for the dual $$(cf-\frac{e^2}4)X^2+(\frac{de}2-bf)XY+(af-\frac{d^2}4)Y^2+(\frac{be}2-cd)X+(\frac{bd}2-ae)Y+(ac-\frac{b^2}4)=0$$ substitute $(X,Y)=(-\frac1{17},\frac2{17}),$ seeing as the corresponence goes through $xX+yY+1=0.$

$\begin{align}&5^2a+5d+f&=0\\&3^2c+3e+f&=0\\&10a+d&=0\\&6c+e&=0\\&\frac{4cf-8bf+16af-e^2+4de-34be+136ae-4d^2+68cd-68bd+1156ac-289b^2}{34^2}&=0\end{align}$

Solving gives the double line through $(5,0)$ and $(0,3)$ or a multiple of $$2601x^2+750xy+7225y^2-26010x-43350y+65025=0.$$ This generalizes.