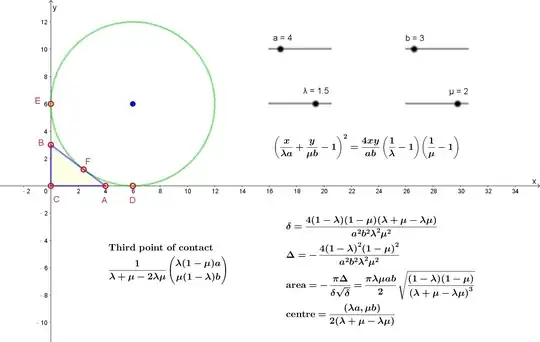
We can think of an incircle and three excircles of a triangle. So the question is : do exellipses exist? Inellipses do exist, and there are a number of studies on it such as the Steiner Ellipse and Marden's Theorem. However, I couldn't find any information on the 'exellipse' ; the ellipse that behaves like an excircle.
Am I getting the name wrong? I expected it to be 'exellipse', but it seems that the word does not exist at all. Also, I would like to find out whether the properties of the incircle and the excircle still holds when it comes to inellipses and 'exellipses'.
The following picture expresses both the inellipse and the 'exellipse' of a triangle. (Sorry for bad resolution.)