Currently reading "Introduction to Graph Theory" by Douglas B. West. I have my doubts whether the following proof I managed to compose is accurate, or if it could be simplified.
"Prove that at any party with six people, there are three mutual acquaintances or three mutual strangers."
Proof. Because acquaintance is a symmetric relation, we can model it using a simple graph $G$ under six vertices with a vertex for each person and an edge for each acquainted pair. Let $C=\{\text{Orange, Blue}\}$ where if pair $(u,v)$ are acquainted then edge $uv \in E(G)$ is colored orange, otherwise blue. Since every pair of people is either acquainted or not, then $G$ must be a complete graph.
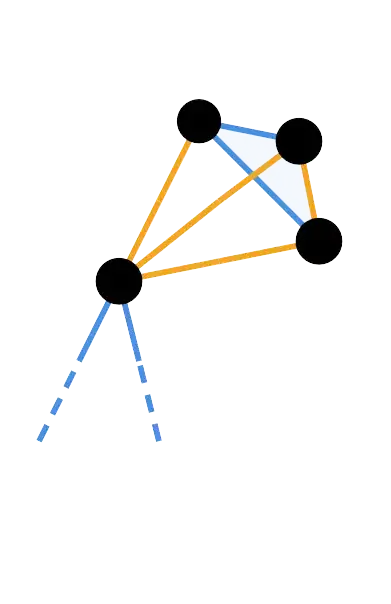
Now, observe that for any vertex $v \in V(G)$ we have that $|N_G(v)|=5$. There must be at least $|C|+1$ edges incident to $v$ of equal coloring because the size of the neighborhood of $v$ is an odd number. Without loss of generality, consider the figure below and choose some vertex $v \in V(G)$.
Recall $G$ is a complete graph so there must exist a 3-vertex subset $S \subseteq V(G)$ where all $u\in S$ is adjacent to $v$ and all edges $uv$ are equally colored. Because $|C|<3$ and the induced subgraph $G[S]\cong K_3$ then at least two edges in $G[S]$ must be equally colored.
If all edges in $G[S]$ are equally colored then all vertices in $S\subseteq V(G)$ are three mutual acquaintances or three mutual strangers. Otherwise, there exist at least one edge $u_iu_j \in E(G[S])$ equally colored as all edges of the form $uv$ inducing a 3-vertex cycle where all vertices are mutually acquainted or mutual strangers. QED.