1

I'm reading introduction to combinatorics and encountered an exercise I couldn't answer

Let S be a set of six points in the plane, with no three of the points collinear. Color either red or blue each of the 15 line segments determined by the points of S. Show that there is at least two triangles determined by points of S which are either a red triangle or a blue triangle.(Both may be red, or both may be blue and one may be red the other bule)

Thanks if you can give me any help.

yuan
  • 141
  • 1
  • 7
  • 2
    Since you're new, I'd like to give you some advice about the site: To get the best possible answers, you should explain what your thoughts on the problem are. That way, people won't tell you stuff you already know, and they can write answers at an appropriate level; also, people tend to be more willing to help if you show that you've tried the problem yourself. Also, some may consider your post rude because it is phrased as a command, not a request for help, so please consider rewriting it. – Zev Chonoles Jul 29 '13 at 00:42
  • It seems as though you might be confused about the question. When they say that "there is at least one triangles determined by points of S that is either a red triangle or a blue triangle", they mean that in any such graph, one of them must exist, but the other doesn't have to. For example, if every line is blue, you can't find a red triangle, but you can definitely find a blue one with any three points. So, you can't make sure that the first triangle exist, because it might not. But if it does not, then we can find the other one. – Ben Grossmann Jul 29 '13 at 00:55
  • Did you see the answers so far? Have you tried something along those lines? – Ben Grossmann Jul 29 '13 at 01:01
  • @yuan I haven't shown that any triangle exists yet. All I've shown is that we have a point, and three lines of the same color coming out of that point. – Ben Grossmann Jul 29 '13 at 01:19
  • I've updated my answer with some pictures, hopefully that clears things up a little – Ben Grossmann Jul 29 '13 at 01:28
  • 2
    Related. – Andrés E. Caicedo Jul 29 '13 at 02:54

3 Answers3

3

To the modified version of your question: we can always find a second triangle, but not a third. The proof is as follows:

We start by acknowledging the first triangle (let's say that it's red), as guaranteed from the previous proof. Choose a point not in that triangle. Following the steps of the original proof, either we have a new triangle, or there are three blue edges from this point to each point on the red triangle.

Now look at the three points outside of the red triangle, supposing that each has three blue edges from each point on the red triangle. If any two of these outside points are connected with a blue edge, we have a blue triangle. Otherwise, the outside points form another red triangle. Either way, we have found a second triangle.

To disprove the guaranteed existence of a third triangle, consider the graph in which these edges are blue and the rest are red. We have two red triangles, but no more.

Ben Grossmann
  • 225,327
  • Good answer to the OP's real question. I have often seen the proof that there is one triangle and a statement that there is another, but no proof for the second. – Ross Millikan Jul 29 '13 at 02:43
  • @RossMillikan Thank you. For the record, the original question was the one-triangle statement. OP then edited the post to ask this follow-up. – Ben Grossmann Jul 29 '13 at 02:49
2

Hint: consider any point on the graph. This point has $5$ protruding line segments, each of which are red or blue. We note that there must be at least $3$ line segments of the same color.

We can show that the points on the end of these $3$ segments form a red or a blue triangle. How?

Hint: Suppose that the three segments we found were red. Let's look at the points on the end of those segments, and the connection from each to the other. If any two are connected with a red line, then we have a red triangle. Draw this to check.

Now, what if none of the two points at the end of these $3$ segments are connected with a red line? Can we say anything about either a red or blue triangle?

Some helpful pictures: We looked at a point $A$, and noticed that whatever colors come out of $A$, we have to have $3$ that are the same

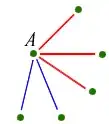
5 lines coming out

We then looked at the three points on the end. If there's a red line between any $2$ of them, then we have a red triangle. What happens if there isn't?

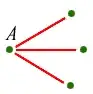
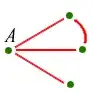
3 of the same color (red in this case) If red edge between them, then red triangle

ANSWER:

There must be a blue triangle Blue triangle

Ben Grossmann
  • 225,327
  • if there isn't exist a red line then there is a blue triangle – yuan Jul 29 '13 at 01:29
  • Exactly. So, we've shown that: 1. you always have three points of the same color (let's say red). 2. If you have three points of the same color, you must have either a red triangle or a blue triangle. 3. Therefore, any graph on six points colored red and blue will have either a red triangle or a blue triangle. – Ben Grossmann Jul 29 '13 at 01:32
  • ok,my question is that if there exist a second triangle(maybe blue,maybe red)? – yuan Jul 29 '13 at 01:34
  • I'm not sure, but I think there must be an example of a graph with only the one triangle. – Ben Grossmann Jul 29 '13 at 01:51
  • To be precisely,the question I post is to proof that the second triangle exists. If you think there be an example of a graph with only one triangle, can you draw it? – yuan Jul 29 '13 at 01:58
  • Well there are certainly graphs that don't have both a red and green triangle. Is that what you want? I'm still seeing if there's one that has exactly one triangle of a single color. What you're asking now goes beyond the scope of your original question, which is simply a statement of the theorem on friends and strangers– http://en.wikipedia.org/wiki/Theorem_on_friends_and_strangers – Ben Grossmann Jul 29 '13 at 02:01
  • If you'd like to ask a new question, you should post it separately. In the mean time, I'll keep looking for a disproof. – Ben Grossmann Jul 29 '13 at 02:02
  • let us continue this discussion in chat – yuan Jul 29 '13 at 02:03
1

This is really a graph theory problem, so there is no need to worry about planar embeddings or collinearity. What you mean is that any 2-coloring of the edges in $K_6$ (complete graph on six vertices) contains a monochromatic triangle.

The classic proof of this is as follows: pick some vertex $v$. There are five vertices connected to it, so three of these edges will have the same color (say, red). The three corresponding vertices will form a monochromatic triangle (why?).

The moral of this exercise is essentially to see how to apply the pigeonhole principle. Whenever you've got only two colors and a lot of edges, look for large collections of monochromatic edges. This is a common theme of Ramsey theory on finite graphs.

Here is another exercise with a similar solution: show that if you 2-color the planar lattice $\mathbb{N}^2$, you must have a monochromatic rectangle. Edit: 2-color the vertices of the lattice, I mean.

Edit: I have removed a crucial step in my proof, since Omnomnomnom has given a very good hint along the lines of "figure out the missing step".

Andrew Poelstra
  • 575
  • very much appreciated. I feel that homework questions require a delicate touch. – Ben Grossmann Jul 29 '13 at 00:58
  • 1
    For the plane lattice question, we can't we color all horizontal edges red and all vertical edges blue? – A.S Jul 29 '13 at 01:35
  • Andrew, for the plane lattice problem, you need to show that for -any- coloring, you can find some monochromatic rectangle. So you don't get to set the colors. – Andrew Poelstra Jul 29 '13 at 02:36
  • 1
    @AndrewPoelstra Right, but I was wondering how coloring horizontal edges red and vertical edges blue fails to generate a counterexample (how does this contain a monochromatic rectangle)...but maybe I misunderstand the question and you're supposed to color the vertices. – A.S Jul 29 '13 at 14:48
  • Oh, you're right! You -were- supposed to color the vertices, but I had a dumb moment and thought that the distinction wouldn't matter. (Because the edges look like a vertex lattice if you zoom out enough, right? ;)). I will edit my original answer. – Andrew Poelstra Jul 29 '13 at 15:18