How to calculate $\int_{-\infty}^\infty\frac{e^x}{1+e^{3x}}dx$ using residues

Question

My original problem was this $$\int_0^\infty\frac1{1+x^3}dx$$I wanted to solve it using the Residue theorem, but the only integrals I could integrate using it are across the entire real line. So I made the substitution $u=\ln x$ to get $$I=\int_{-\infty}^\infty\frac{e^x}{1+e^{3x}}dx=\operatorname{Re}\left(2\pi i\sum_{k=\frac{\pi i}3+2n\pi i}\operatorname{Res}_{z=k}\left(\frac{e^z}{1+e^{3z}}\right)\right)$$By integration along the semicircular contour, and the integral along the arc is well-known to go to zero. These poles are of first order, so $$\operatorname{Res}_{z=k}\left(\frac{e^z}{1+e^{3z}}\right)=\lim_{z\rightarrow k}\frac{e^z(z-k)}{1+e^{3z}}=\frac1{3e^{2k}}$$So the answer should be $$I=\frac{2\pi}3\operatorname{Re}\left(\sum_{k=0}^\infty e^{-2(\pi i/3+2k\pi i)}\right)$$I know that the real answer is $I=\frac{2\pi}{3\sqrt 3}$ and so the infinite series must evaluate to $\frac1{\sqrt 3}$ for my answer to be right. However, according to Wolfram Alpha, the infinite series diverges. So I am not sure what exactly I have done wrong. I was thinking that maybe this is because I only need to choose $\frac{\pi i}3$ and $\pi i$ as poles, but I have no other idea.

Edit: It is very clear that my question is not a duplicate because I am wondering why my answer diverges while the duplicate only asks for how to solve it. I added tags to make it clear.

Answer 1

There are a few mistakes here. I propose a way to correctly use contour integration - using the integrand in the form you give - at the bottom of the post.

More important points:

It is not true that the residue theorem can only come in handy for integrals over the whole real line. That remark applies for the semicircular contour method but there are others; my personal favourite way to integrate (when it applies) is to use a dogbone or Hankel contour method and these may appear even for bounded domains like $[-1,1]$.

The real thing I want to talk about:

Just because 'usually' the arc integral vanishes doesn't mean it always will! In fact, it doesn't vanish. You always, always need to do a sanity check on the asymptotics. The standard trick with $\sin(t)\ge\frac{2}{\pi}t$ on $[0,\pi/2]$ tells you that integrating $\int e^zf(z)$ over those large semicircular arcs gives you something roughly of size $\int_0^{\pi}|f(Re^{it})|\,\mathrm{d}t$, $R$ the radius. Ok, so to expect this vanish we should definitely make sure $f$ - here, $f(z)=(1+e^{3z})^{-1}$ - decays sufficiently well as you go out to the upper half plane. But in this case that's not obvious; $f$ attains $\infty$ infinitely often as we move out to the upper half plane! Ok sure, you could rig $R=\frac{2\pi i}{3}(1+N)$, $N$ a large integer, to try to avoid the poles as much as possible, but then we still don't observe decay; $|f|\approx2$ near the peak of the semicircular arc. It is not at all clear that the integral over the semicircular arc vanishes. It doesn't follow from the standard observations, as far as I can tell: moral, don't be too hasty with "everyone knows it vanishes"!

In fact, I can prove to you it doesn't vanish - it doesn't even converge! Simply observe that the integral over the real line converges, whereas the (corrected) residue series still purely consists of summands of type $e^{i\theta}$ where $\theta$ is real; these do not tend to zero - are constantly of unit modulus - so the series diverges by the simplest divergence test.

Less important points:

Why take the real part of the residues? The closed contour integral is exactly equal to the residue sum, real part and imaginary part altogether, and if the other arc integral vanishes then there is an exact equality $\int_{-\infty}^\infty=\sum\mathrm{Res}$ (maybe taking a limit somewhere in there) but certainly no real part operator. If the right hand side is nonreal, and the left hand side is a pure real integrand, then there's a mistake.

Now for the roots. $e^{3z}=-1$ iff. $3z=\pi i+2\pi in$ for $n\in\Bbb Z$ iff. $z=\frac{\pi i}{3}+\frac{2\pi i}{3}n$ - you missed the "$n/3$" aspect.

---

Alright, so the semicircular arc doesn't work. We can still do something; a nice trick is to exploit the periodicity of the exponential. If $x\mapsto x+\frac{2\pi i}{3}$, the integrand transforms like $f(x)\mapsto e^{2\pi i/3}f(x)$, thus: $$(1-e^{2\pi i/3})I=\oint_{\text{Large boxes of height $2\pi/3$}}=2\pi i\cdot\mathrm{Res}\left(f;\frac{\pi i}{3}\right)$$Where now, truly, the 'error' terms - the short integrals of type $\int_R^{R+2\pi i/3}$ and $\int_{-R}^{-R+2\pi i/3}$ - really do vanish by an easy check. The integral coming back down the final edge of the box, $R+2\pi i/3\to -R+2\pi i/3$, is just a multiple of $I$ by my observation.

There is only one pole enclosed in my contour, which is also nice. The residue computation is as you say, so we find: $$I=\frac{2\pi i}{1-e^{2\pi i/3}}\cdot\frac{1}{3e^{2\pi i/3}}=\frac{\pi}{3}\csc(\pi/3)=\frac{2\pi}{3\sqrt{3}}$$Here's an image:

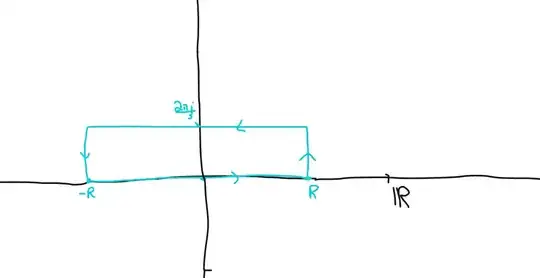
And we take limits in $R\to\infty$.

Answer 2

First, I would convert this problem back to its original form.

$\int_0^\infty \frac {1}{1+x^3}\ dx$

Now we will form a contour that includes the real line, an arc of radius $R$ taking the limit as $R$ approaches infinity, and a line from the endpoint of this arc back to the origin.

What will be the endpoint of the arc?

$\frac {1}{1+z^3}$ has poles at $-1, e^{\frac {\pi}{3} i}, e^{-\frac {\pi}{3} i}$

We want to get one of these poles inside our contour.

I propose taking 1 third of a circle. i.e.$\ \theta = \frac {2\pi}{3}$

We will have

$\oint_\gamma \frac {1}{1+z^3}\ dz = \lim_\limits{R \to \infty} \int_0^R \frac {1}{1+x^3} \ dx + \int_0^\frac {2\pi}{3} \frac {iRe^{i\theta}}{1+(Re^i\theta)^3} \ d\theta + \int_R^0 \frac {e^{\frac {2\pi}{3}i}}{1+(te^{\frac {2\pi}{3}})^3} \ dt$

$\left|\lim_\limits{R\to \infty} \int_0^\frac {2\pi}{3} \frac {iRe^{i\theta}}{1+(Re^i\theta)^3} \ d\theta\right| < \lim_\limits {R\to \infty}\frac {2\pi}{3}\left|\frac {iRe^{i\theta}}{1+(Re^i\theta)^3}\right| < \lim_\limits {R\to \infty}\frac {2\pi}{3R^2} = 0$

$\int_0^R \frac {1}{1+x^3} \ dx + \int_R^0 \frac {e^{\frac {2\pi}{3}i}}{1+(te^{\frac {2\pi}{3}})^3} \ dt = (1-e^{\frac {2\pi}{3}i})\int_0^R \frac {1}{1+x^3} \ dx$

$\oint_\gamma \frac {1}{1+z^3}\ dz = (1-e^{\frac {2\pi}{3}i})\int_0^\infty \frac {1}{1+x^3} \ dx\\ \int_0^\infty \frac {1}{1+x^3} \ dx = \frac {1}{1-e^{\frac {2\pi}{3}i}}\oint_\gamma \frac {1}{1+z^3}\ dz$

Evaluating the residue at $e^{\frac {\pi}{3}i}$

$\text{Res}_{z = e^{\frac {2\pi}{3}i}} \frac {1}{1+z^3} = \frac {1}{3e^{\frac {2\pi}{3}i}}=\frac {e^{\frac {4\pi}{3}i}}{3}$

$\int_0^\infty \frac {1}{1+x^3} \ dx = (2\pi i)\frac {1}{1-e^{\frac {2\pi}{3}i}}\frac {e^{\frac {4\pi}{3}i}}{3}\\ (2\pi i)\frac {e^{-\frac {\pi}{3}i}}{e^{-\frac {\pi}{3}i}-e^{\frac {\pi}{3}i}}\frac {e^{\frac {4\pi}{3}i}}{3}\\ \pi\frac {2i}{e^{-\frac {\pi}{3}i}-e^{\frac {\pi}{3}i}}\frac {e^{\pi i}}{3}= \frac {\pi}{3\sin \frac {\pi}{3}} = \frac {2\pi}{3\sqrt 3}$