Strange contour integral: $\int_0^{\infty} \frac{e^{\cos(x)}\sin(\sin(x))}{x} dx$ using residue calculus

Question

I am interested in calculating $$\int_0^{\infty} \frac{e^{\cos(x)}\sin(\sin(x))}{x} dx$$ using the residue calculus. I thought the thing to do was to consider $$f(z) = \frac{e^{e^{iz}}}{z}$$ since $\textrm{Im}(f(x)) = \frac{e^{\cos(x)}\sin(\sin(x))}{x}$ and integrate on an indented semicircular contour with inner radius $\epsilon$, outer radius $R$ and let $\epsilon \to 0, R \to \infty$. I calculated $$\lim_{\epsilon \to 0}\int_0^{\pi} f(\epsilon e^{i\theta})i\epsilon e^{i\theta} d\theta$$ using that $f(z) = \frac{e}{z} + O(z)$ near $0$, but the problem is that the integral along the large semicircle does not vanish as $R \to \infty$. Actually calculating this integral seems hopeless. Any hints?

Answer 1

As shown by @eyeballfrog, $$\int_0^{\infty} \frac{e^{\cos(x)}\sin(\sin(x))}{x} dx =\int_0^\pi \frac{\sin[\sin(u)]}{\sin(u)}\sin^2\left(\frac{u}{2}\right)e^{-\cos(u)}du$$

Further manipulating: $$\begin{align} \int_0^\pi \frac{\sin[\sin(u)]}{\sin(u)}\sin^2\left(\frac{u}{2}\right)e^{-\cos(u)}du &=\int_0^\pi \frac{\sin[\sin(u)]}{\sin(u)}\left(\frac{1-\cos u}{2}\right)e^{-\cos(u)}du \\ &=\frac12\int_{-\pi}^\pi \frac{\sin[\sin(u)]}{\sin(u)}\left(\frac{1-\cos u}{2}\right)e^{-\cos(u)}du \\ &=\frac14\Im\int_{-\pi}^\pi \frac{1-\cos u}{\sin(u)}e^{-\cos(u)+i\sin u}du \\ &=\frac14\Im\int_{-\pi}^\pi \frac{1-\cos u}{\sin(u)}\exp(-e^{-iu})du \\ &=-\frac14\Im\int_{-\pi}^\pi \frac{1-\cos u}{\sin(u)}\exp(-e^{iu})du \\ \end{align} $$

Let $z=e^{iu}$, then $$\begin{align} \int_0^\pi \frac{\sin[\sin(u)]}{\sin(u)}\sin^2\left(\frac{u}{2}\right)e^{-\cos(u)}du &=-\frac14\Im\int_{-\pi}^\pi \frac{2-2\cos u}{2\sin(u)}\exp(-e^{iu})du \\ &=-\frac14\Im\oint_{|z|=1} \frac{2-z-z^{-1}}{(z-z^{-1})/i}\exp(-z)\frac{dz}{iz} \\ &=\frac14\Im\oint_{|z|=1} \frac{z^2-2z+1}{z^2-1}\frac{e^{-z}}z dz\\ &=\frac14\Im\underbrace{\oint_{|z|=1} \frac{z-1}{z+1}\frac{e^{-z}}z dz}_{I}\\ \end{align} $$

Note that the contour integral has to be understood in the Cauchy principal value sense, since a pole lies on the path of integration.

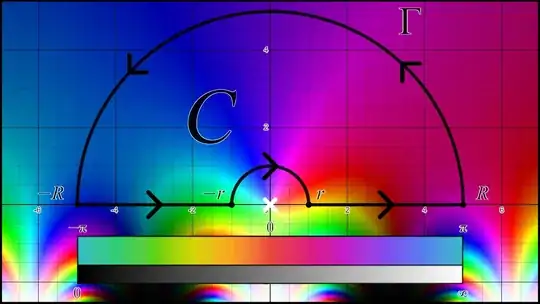
Consider the contour $C$, a unit circle with a semicircle indent to the right at $z=-1$.

By residue theorem, $$\oint_C \frac{z-1}{z+1}\frac{e^{-z}}z dz=2\pi i\operatorname*{Res}_{z=0}\frac{z-1}{z+1}\frac{e^{-z}}z$$ $$\implies I+\int_{\text{indent}}\frac{z-1}{z+1}\frac{e^{-z}}z dz=-2\pi i$$

Since the indent is a semicircle and goes clockwisely, it is not difficult to prove that $$\int_{\text{indent}}\frac{z-1}{z+1}\frac{e^{-z}}z dz=-\frac12\cdot 2\pi i\operatorname*{Res}_{z=-1}\frac{z-1}{z+1}\frac{e^{-z}}z=-2\pi i\cdot e$$

Hence, $$I=2\pi i (e-1)$$

As a result, $$\int_0^{\infty} \frac{e^{\cos(x)}\sin(\sin(x))}{x} dx=\frac\pi 2(e-1)$$ which has been confirmed numerically.

Answer 2

(A few years late, but I just saw this a few hours ago.)

Rewrite the integral as $$ \begin{align} I &:= \int_{0}^{\infty}\frac{e^{\cos x}\sin\left(\sin x\right)}{x}dx \\ &= \frac{1}{2}\int_{-\infty}^{\infty}\frac{e^{\cos x}\sin\left(\sin x\right)}{x}dx \\ &= \frac{1}{2}\int_{-\infty}^{0}\Im\left(\frac{\exp\left(e^{ix}\right)}{x}\right)dx+\frac{1}{2}\int_{0}^{\infty}\Im\left(\frac{\exp\left(e^{ix}\right)}{x}\right)dx \\ &= \frac{1}{2}\lim_{R\to\infty}\lim_{r\to0^+}\Im\int_{-R}^{-r}\left(\frac{\exp\left(e^{ix}\right)}{x}\right)dx+\frac{1}{2}\lim_{R\to\infty}\lim_{r\to0^+}\Im\int_{r}^{R}\left(\frac{\exp\left(e^{ix}\right)}{x}\right)dx\, \end{align} $$

where $0 < r \ll R$.

Let $\displaystyle f(z) = \frac{\exp\left(e^{iz}\right)}{z}$. There is a simple pole at $z=0$ because the principal part of the Laurent expansion of $f(z)$ is $\displaystyle \frac{e}{z}$. We can take the OP's idea and construct this contour.

(I forgot to label the small circular arc $\gamma$.) By Cauchy's Integral Theorem, we write $\displaystyle \oint_C f(z)dz$ as

$$ 0 = \int_{-R}^{-r}f(z)dz + \int_{\gamma}f(z)dz + \int_r^R f(z)dz + \int_{\Gamma}f(z)dz\,. $$

We can avoid divergence issues by equating $\Im$ first, applying the limits, then multiplying by $\displaystyle \frac{1}{2}$ like

$$ 0 = I + \frac{1}{2}\lim_{r\to0^+} \Im \int_{\gamma} f(z)dz + \frac{1}{2}\lim_{R\to\infty} \Im \int_{\Gamma}f(z)dz\,. $$

We solve the integral over $\gamma$ like this.

$$ \lim_{r\to0^+} \Im \int_{\gamma} \frac{\exp\left(e^{iz}\right)}{z}dz = -\Im i \pi\mathop{\mathrm{Res}}_{z=0} \frac{\exp\left(e^{iz}\right)}{z} = -\pi \Re \lim_{z\to0}(z-0)\cdot\frac{\exp\left(e^{iz}\right)}{z} = -\pi e \,. $$

To solve the other contour integral, we can first rewrite it as

$$ \begin{align} \Im \int_{\Gamma} \frac{\exp\left(e^{iz}\right)}{z}dz &= \Im \int_{\Gamma} \frac{1}{z} \sum_{n=0}^{\infty} \frac{e^{niz}}{n!}dz \\ &= \Im \sum_{n=0}^{\infty}\frac{1}{n!}\int_{\Gamma}^{ }\frac{e^{niz}}{z}dz \tag{1}\\ &= \Im \sum_{n=0}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\frac{\exp\left(niRe^{it}\right)}{Re^{it}}iRe^{it}dt \\ &= \Re \sum_{n=0}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\exp\left(niRe^{it}\right)dt \\ &= \Re \frac{1}{0!}\int_{0}^{\pi}\exp\left(0\cdot iRe^{it}\right)dt + \Re \sum_{n=1}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\exp\left(niRe^{it}\right)dt \,. \\ \end{align} $$

For $(1)$, since $\exp(e^{iz})$ is entire, its radius of convergence is $\infty$. Note that $\Gamma$ is inside the circle of convergence of the infinite series, which justifies the $\sum$ and $\int$ swap.

The first integral from that last equality equals $\pi$. We bound the second integral like $$ \begin{align} 0 &\leq \left|\Re\sum_{n=1}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\exp\left(niRe^{it}\right)dt\right| \\ &\leq \left|\sum_{n=1}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\exp\left(niRe^{it}\right)dt\right| \\ &\leq \sum_{n=1}^{\infty}\frac{1}{n!}\left|\int_{0}^{\pi}\exp\left(niRe^{it}\right)dt\right| \\ &\leq \sum_{n=1}^{\infty}\frac{1}{n!}\int_{0}^{\pi}\left|\exp\left(niRe^{it}\right)\right|dt \\ &= \sum_{n=1}^{\infty}\frac{1}{n!}\int_{0}^{\pi}e^{-Rn\sin t}dt \\ &< \sum_{n=1}^{\infty}\frac{1}{n!} \cdot \frac{\pi}{Rn}\,. \tag{2} \\ \end{align} $$

For $(2)$, we use Jordan's Inequality to find an upper bound tight enough for that integral.

We take $R \to \infty$ and use the Squeeze Theorem to show that the second integral converges to $0$. We eventually conclude that

$$ \lim_{R\to\infty}\Im \int_{\Gamma} f(z)dz = \pi\,. $$

Finally, $$ \begin{align} 0 &= I - \frac{1}{2}\pi e + \frac{1}{2}\pi \\ \implies I &= \frac{\pi}{2} (e-1) \\ \end{align} $$

and we're finished!

Answer 3

Partial answer

This transform gives you a finite integral that is much more amenable to numeric methods:

\begin{multline} \int_0^\infty \frac{e^{\cos(x)}\sin[\sin(x)]}{x}dx \\ = \sum_{n=0}^\infty \left(\int_{2n\pi}^{(2n+1)\pi}\frac{e^{\cos(x)}\sin[\sin(x)]}{x}dx+\int_{(2n+1)\pi}^{2(n+1)\pi}\frac{e^{\cos(x)}\sin[\sin(x)]}{x}dx\right) \\ = \sum_{n=0}^\infty \left(\int_{0}^{\pi}\frac{e^{-\cos(u)}\sin[\sin(u)]}{(2n+1)\pi -u}du-\int_{0}^{\pi}\frac{e^{-\cos(u)}\sin[\sin(u)]}{(2n+1)\pi + u}du\right) \\ = \int_0^\pi e^{-\cos(u)}\sin[\sin(u)]\left[\sum_{n=0}^\infty \frac{2u}{(2n+1)^2\pi^2-u^2}\right]du \\ = \frac{1}{2}\int_0^\pi e^{-\cos(u)}\sin[\sin(u)]\tan\left(\frac{u}{2}\right)du = \int_0^\pi \frac{\sin[\sin(u)]}{\sin(u)}\sin^2\left(\frac{u}{2}\right)e^{-\cos(u)}du \end{multline} This last integral has a bounded integrand within the domain of integration, and thus is good for numeric methods.

We can also get rather concise form of the integral using a trig transform: $$ \int_0^\infty \frac{e^{\cos(x)}\sin[\sin(x)]}{x}dx = \frac{1}{2}\int_0^\pi e^{-\cos(u)}\sin[\sin(u)]\tan\left(\frac{u}{2}\right)du = \int_{-1}^1\frac{e^{-y}\sin(\sqrt{1-y^2})}{2(1+y)}dx $$ but Mathematica still doesn't want to do it analytically. It does have branch points at the ends of the interval, so perhaps this kind of contour integration could go somewhere.