It's impossible.
We'll show this by exhibiting a subset of the large disk that the smaller disks cannot cover more than $99.91\%$ of even if we count coverings with multiplicity, which is much easier to check. Specifically, we'll choose a set of four extremely thin rings centered around the origin, tuning their relative thicknesses to make the impossibility proof work out. We also renormalize so the central disk has radius $1$ and the smaller disks have radii in the set $R = \{1/\sqrt{2}, 1/\sqrt{3},\ldots,1/\sqrt{7}\}$.
By the Law of Cosines, the fraction of an origin-centered ring of radius $x$ covered by a disk of radius $r$ whose center is distance $d$ from the origin is
$$\frac{\arccos\left(\frac{d^2+x^2-r^2}{2dx}\right)}{\pi}$$
where we cap the output of $\arccos()$ if its input lies outside the range $[-1,1]$.
If we look at $x=1$, ie the perimeter of the disk, we can look at the fraction of perimeter covered by each disk as a function of $d$:

Adding up the maxima of these fractions for each $r\in R$ gives us a total covering fraction of $1.0173$, which doesn't rule things out as yet but suggests that we don't have much room to maneuver away from the perimeter.
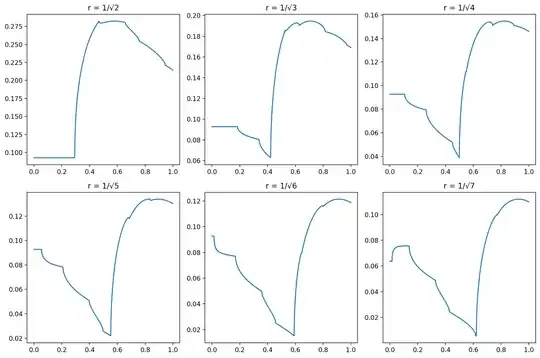
Generalizing a bit, we'll add three more rings, so we look at $X =[x_1,x_2,x_3,x_4=1]$. We'll then weight these rings by $W = [w_1,w_2,w_3,w_4]$, where we normalize $W$ to sum to $1$. If we can find values of $X$ and $W$ such that
$$\sum_{r\in R}\max_{d\in[0,1+r]}\left(\sum_{i=1}^4\frac{w_i}{\pi}\arccos\left(\frac{d^2+x_i^2-r^2}{2dx_i}\right)\right) < 1$$
then we'll know the problem is impossible, since in any valid solution the sum of covered fractions along each ring (and hence any weighted sum thereof) would need to exceed 1. (We could also think of this as using an equally-weighted sum across a 2D region, where we each turn each ring into an annulus of thickness $\epsilon w_i/x_i$ - for small enough $\epsilon$, this will have behavior arbitrarily close to the above setting.)
I fed this function into scipy.optimize.minimize with the constraint that all weights be nonnegative and it spit out the solution $X=[0.05,0.2384,0.3932,1], W=[0.01785, 0.04577, 0.02912, 0.90725]$. With these parameters the maximum weighted sum is around $0.999005$. The weighted scores for each disk as a function of $d$ are graphed below: