What makes this interesting is how to obtain the joint distribution of the points on the circle. Writing three uniformly random points in spherical coordinates and trying to obtain the corresponding angles on the circle leads to a convoluted mess, so let’s try to go the other way and calculate the Jacobian for three points parameterized using the circle they form.
Let the circle be parallel to the $x$-$y$ plane at polar angle $\theta$, with three points at azimuthal angles $\varphi_i$, so their coordinates are $\vec r_i=(\sin\theta\cos\varphi_i,\sin\theta\sin\varphi_i,\cos\theta)$. To move this configuration into general position, we can rotate the $z$ axis into an arbitrary direction, e.g. by applying rotations about the $y$ axis and then the $x$ axis, through $\psi$ and $\xi$, say, for a total of six parameters, as required.
Consider the infinitesimal changes along the six orthogonal unit vectors in the directions $\frac{\partial\vec r_i}{\partial\theta}$ and $\frac{\partial\vec r_i}{\partial\varphi_i}$ when we change these parameters. That’s six changes for six parameters, so we get a $6\times6$ Jacobian. Label the columns by $\varphi_1,\varphi_2,\varphi_3,\theta,\psi,\xi$ and the rows by $\frac{\partial\vec r_1}{\partial\varphi_1},\frac{\partial\vec r_2}{\partial\varphi_2},\frac{\partial\vec r_3}{\partial\varphi_3},\frac{\partial\vec r_1}{\partial\theta},\frac{\partial\vec r_2}{\partial\theta},\frac{\partial\vec r_3}{\partial\theta}$.
Since we only need the dependence of the joint distribution on the $\varphi_i$, I’m going to drop all factors that don’t depend on them. Then the upper left $3\times3$ minor is the identity, and the one below it is zero, since changing $\varphi_i$ only causes a change along the corresponding vector $\frac{\partial\vec r_i}{\partial\varphi_i}$ and the magnitude of that change is the same for all points (namely $\sin\theta$) and doesn’t depend on the $\varphi_i$.
Thus, to get the determinant of the Jacobian, we can use Laplace expansion along the first three columns, which leaves us with the determinant of the lower right $3\times3$ minor.
The first column of that minor, which contains the changes with $\theta$ along $\frac{\partial r_i}{\partial\theta}$, has all entries $1$. To obtain the other two columns, consider the effect of the infinitesimal generators $\pmatrix{0&0&\epsilon\\0&0&0\\-\epsilon&0&0}$ and $\pmatrix{0&0&0\\0&0&\epsilon\\0&-\epsilon&0}$ of rotations about the $y$ and $x$ axis, respectively, on the $\vec r_i$:
$$
\pmatrix{0&0&\epsilon\\0&0&0\\-\epsilon&0&0}\pmatrix{\sin\theta\cos\varphi_i\\\sin\theta\sin\varphi_i\\\cos\theta}=\epsilon\pmatrix{\cos\theta\\0\\-\sin\theta\cos\varphi_i}\;,
\\[18pt]
\pmatrix{0&0&0\\0&0&\epsilon\\0&-\epsilon&0}\pmatrix{\sin\theta\cos\varphi_i\\\sin\theta\sin\varphi_i\\\cos\theta}=\epsilon\pmatrix{0\\\cos\theta\\-\sin\theta\sin\varphi_i}\;.
$$
Taking the scalar product with the unit vector $\frac{\partial r_i}{\partial\theta}=(\cos\theta\cos\varphi_i,\cos\theta\sin\varphi_i,-\sin\theta)$ yields $\cos\varphi_i$ and $\sin\varphi_i$, respectively, so the lower right minor is
$$\begin{vmatrix}1&\cos\varphi_1&\sin\varphi_1\\1&\cos\varphi_2&\sin\varphi_2\\1&\cos\varphi_3&\sin\varphi_3\end{vmatrix}\;.$$
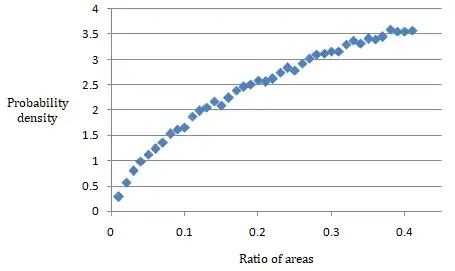
Interestingly, this happens to be proportional to the area of the triangle formed by the points, whose ratio to the area of the circle is, as Blitzer noted in a comment, given by
$$\frac2\pi\left|\sin\frac\alpha2\sin\frac\beta2\sin\frac\gamma2\right|=\frac1{2\pi}|\sin \alpha+\sin\beta+\sin\gamma|\;,$$
where $\alpha=\varphi_2-\varphi_1$, $\beta=\varphi_3-\varphi_2$ and $\gamma=\varphi_1-\varphi_3$.
Thus, the expected value of this ratio is
$$
\mathsf E\left[\frac\triangle\bigcirc\right]
=
\frac1{2\pi}\cdot\frac{\iiint(\sin\alpha+\sin\beta+\sin\gamma)^2\mathrm d\varphi_1\mathrm d\varphi_2\mathrm d\varphi_3}{\iiint|\sin\alpha+\sin\beta+\sin\gamma|\mathrm d\varphi_1\mathrm d\varphi_2\mathrm d\varphi_3}\;.
$$
In the numerator, the integral over the mixed terms vanishes, leaving
$$
\iiint\left(\sin^2\alpha+\sin^2\beta+\sin^2\gamma\right)\mathrm d\varphi_1\mathrm d\varphi_2\mathrm d\varphi_3=\frac32(2\pi)^3\;.
$$
In the denominator, by symmetry we can restrict to the $\varphi_i$ ordered counterclockwise (and thus $\alpha$, $\beta$, $\gamma$ positive) to get rid of the absolute value and obtain
\begin{eqnarray*}
\iiint|\sin\alpha+\sin\beta+\sin\gamma|\,\mathrm d\varphi_1\mathrm d\varphi_2\mathrm d\varphi_3
&=&
2\cdot3\cdot2\pi\int_0^{2\pi}\int_0^{2\pi-\alpha}\sin\alpha\,\mathrm d\beta\,\mathrm d\alpha
\\
&=&
2\cdot3\cdot2\pi\int_0^{2\pi}(2\pi-\alpha)\sin\alpha\,\mathrm d\alpha
\\
&=&
2\cdot3\cdot(2\pi)^2\;.
\end{eqnarray*}
Thus, with
$$
\frac1{2\pi}\cdot\frac{\frac32(2\pi)^3}{2\cdot3\cdot(2\pi)^2}=\frac14\;,
$$
your numerical findings are confirmed.