How to solve $\int_0^\infty\frac1{(ti+1)^2(e^{2\pi t}-1)}-\frac1{(-ti+1)^2(e^{2\pi t}-1)}dt$

Question

Happy New Year! Using the Abel-Plana formula on the Basel sum, I found that $$-i\frac{\pi^2-9}6=\int_0^\infty\frac1{(ti+1)^2(e^{2\pi t}-1)}-\frac1{(-ti+1)^2(e^{2\pi t}-1)}dt$$ How do I solve this integral without the knowledge of the Abel Plana summation formula?

Answer 1

Taking the common denominator of the expression in RHS, we get:

$$I = \int_0^{\infty} \frac{1}{e^{2\pi t}-1} \cdot \frac{-4it}{(1+t^2)^2} dt = -i\cdot \int_0^{\infty} \frac{4tdt}{(1+t^2)^2\cdot (e^{2\pi t} -1)}$$

Now, from Binet's second formula for the digamma function, we have:

$$\psi(z)=\log(z)-\frac{1}{2z}-2\int_0^\infty \frac{x}{(x^2+z^2)(e^{2\pi x}-1)}dx$$

Differentiating the equation once with respect to $z$, we get

$$\psi^1(z) = \frac{1}{z} + \frac{1}{2z^2} + z\cdot \int_0^{\infty} \frac{4x}{(x^2+z^2)^2\cdot (e^{2\pi x} -1)} dx$$

For $z=1$, we get

$$\psi^1(1) = \frac{\pi^2}{6} = \frac{3}{2} + \int_0^{\infty} \frac{4xdx}{(1+x^2)^2\cdot (e^{2\pi x} -1)}$$

Thus we get

$$\int_0^{\infty} \frac{4xdx}{(1+x^2)^2\cdot (e^{2\pi x}-1)} = \frac{\pi^2-9}{6}$$

And thus we arrive at the result:

$$ I = -i\cdot \frac{\pi^2-9}{6}$$

Answer 2

Without using the Abel-Plana Formula, we will prove the following equality.

$$ \bbox[15px,#FFFAFD,border:6px groove#60007C]{\int_0^\infty\left(\frac1{(ti+1)^2(e^{2\pi t}-1)}-\frac1{(-ti+1)^2(e^{2\pi t}-1)}\right)dt = i\frac{9-\pi^{2}}{6}} $$

Proof. Let $\mathcal{I}$ be the integral in question. Using the Laplace Transform,

$$ \frac{1}{2}\int_{0}^{\infty}ye^{-y}\sin\left(xy\right)dy=\frac{x}{\left(1+x^{2}\right)^{2}}\,, $$

we get

$$ \begin{align} \mathcal{I} &:= \int_0^\infty\left(\frac1{(ti+1)^2(e^{2\pi t}-1)}-\frac1{(-ti+1)^2(e^{2\pi t}-1)}\right)dt \\ &= -4i\int_{0}^{\infty}\frac{x}{\left(e^{2\pi x}-1\right)\left(1+x^{2}\right)^{2}}dx \\ &= -4i\int_{0}^{\infty}\int_{0}^{\infty}\frac{ye^{-y}\sin\left(xy\right)}{2e^{2\pi x}-2}dydx \\ &= -4i\overbrace{\int_{0}^{\infty}\int_{0}^{\infty}\frac{ye^{-y}\sin\left(xy\right)}{2e^{2\pi x}-2}dxdy}^\text{Fubini's Theorem} \\ &= -2i\int_{0}^{\infty}ye^{-y}\int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dxdy\,. \\ \end{align} $$

We write the inner integral as

$$ \int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dx = \lim_{L\,\to\,\infty}\lim_{r\,\to\,0^{+}}\Im\int_{r}^{L}\frac{e^{iyx}}{e^{2\pi x}-1}dx\,. $$

In the next section, we will use contour integration to prove

$$ \bbox[10px,#F7FFDF]{\int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dx = \frac{1}{4}\coth\left(\frac{y}{2}\right)-\frac{1}{2y}\,.} $$

---

Define a holomorphic function

$$ f: \mathbb{C}\,\backslash\left\{n \in \mathbb{Z}\,:\,in\right\} $$ $$ z\mapsto \frac{e^{iyz}}{e^{2\pi z}-1} $$

and a contour $C$ that travels counterclockwise through the union of sets, in order,

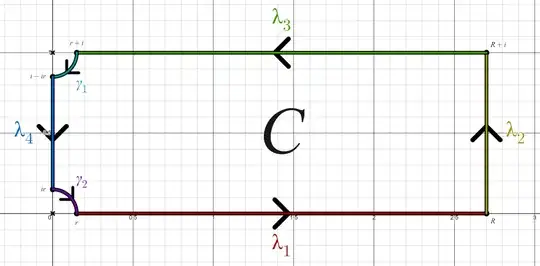
$$ \begin{align} \color{#9E0000}{\lambda_1} &:= [r,L] \\ \color{#9E9300}{\lambda_2} &:= \left\{L+it\,:\,t\in[0,1]\right\}\\ \color{#3F9E00}{\lambda_3} &:= \left\{i-t\,:\,t\in[-L,-r]\right\}\\ \color{#00989E}{\gamma_1} &:= \left\{re^{-it}+1\,:\,t\in\left[0,\frac{\pi}{2}\right]\right\}\\ \color{#0062C3}{\lambda_4} &:= \left\{-it\,:\,t\in[r-1,-r]\right\}\\ \color{#68009E}{\gamma_2} &:= \left\{-re^{-it}\,:\,t\in\left[\frac{\pi}{2},\pi\right]\right\}\,.\\ \end{align} $$

Here, we let $\displaystyle 0<r<\frac{1}{2}\ll L$. I've provided a visual down below that matches exactly what the union of sets is, down to the exact RGB/hexadecimal colors.

(I accidentally used $R$ instead of $L$. Oops :P...)

Integrating over these sets, we have

$$ \oint_{C}f = \int_{\color{#9E0000}{\lambda_1}}f + \int_{\color{#9E9300}{\lambda_2}}f + \int_{\color{#3F9E00}{\lambda_3}}f + \int_{\color{#00989E}{\gamma_1}}f + \int_{\color{#0062C3}{\lambda_4}}f + \int_{\color{#68009E}{\gamma_2}}f\,. $$

Because $f$ is holomorphic on the simply connected open domain $\mathbb{C}\,\backslash\left\{n \in \mathbb{Z}\,:\,in\right\}$, $C$ is homologous to $0$, and $C$ is a piecewise, smooth, and closed loop, we use Cauchy's Integral Theorem to get

$$ \oint_{C}f = 0\,. $$

Applying $\displaystyle \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im$ on both sides, we get

$$ 0 = \int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dx + \lim_{L\,\to\,\infty}\Im\int_{\color{#9E9300}{\lambda_2}}f + \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im\int_{\color{#3F9E00}{\lambda_3}}f + \lim_{r\,\to\,0^+}\Im\int_{\color{#00989E}{\gamma_1}}f + \lim_{L\,\to\,\infty}\Im\int_{\color{#0062C3}{\lambda_4}}f + \lim_{r\,\to\,0^+}\Im\int_{\color{#68009E}{\gamma_2}}f\,. $$

Now we evaluate each of these contour integrals.

For $\displaystyle \lim_{L\,\to\,\infty}\Im\int_{\color{#9E9300}{\lambda_2}}f$, I'll leave that as an exercise for your practice (and because I'm lazy). You can see similar examples here and here. As the vertical line segment gets farther away, we see that the behavior of the contour integral is

$$\lim_{L\,\to\,\infty}\Im\int_{\color{#9E9300}{\lambda_2}}f = 0\,.$$

Letting $z \in \color{#3F9E00}{\lambda_3}$, we evaluate $\displaystyle \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im\int_{\color{#3F9E00}{\lambda_3}}f$ as

$$ \begin{align} \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im\int_{\color{#3F9E00}{\lambda_3}}f &= \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im \int_{-L}^{-r}f(i-t)d(i-t) \\ &= \lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\Im \int_{-L}^{-r}\frac{e^{iy\left(i-t\right)}}{e^{2\pi\left(i-t\right)}-1}d\left(i-t\right) \\ &= -e^{-y}\lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\int_{-L}^{-r}\frac{\Im\left(e^{-iyt}\right)}{e^{-2\pi t}-1}dt \\ &\overset{-t\,\mapsto\,t}= -e^{-y}\lim_{\substack{L\,\to\,\infty \\ r\,\to\,0^+}}\int_{r}^{L}\frac{\sin\left(yt\right)}{e^{2\pi t}-1}dt \\ &= -e^{-y}\int_{0}^{\infty}\frac{\sin\left(yt\right)}{e^{2\pi t}-1}dt\,. \end{align} $$

As the top quarter-circle shrinks towards the simple pole at $z = i$, we evaluate $\displaystyle \lim_{r\,\to\,0^+}\Im\int_{\color{#00989E}{\gamma_1}}f$ as

$$ \begin{align} \lim_{r\,\to\,0^+}\Im\int_{\color{#00989E}{\gamma_1}}f &= \Im\left(-\frac{i\pi}{2}\mathop{\mathrm{Res}}_{z\,=\,i}\frac{e^{iyz}}{e^{2\pi z}-1}\right) \\ &= -\frac{\pi}{2}\lim_{z\,\to\,i}\frac{e^{iyz}}{\frac{d}{dz}\left(e^{2\pi z}-1\right)} \\ &= -\frac{1}{4e^{y}}\,. \\ \end{align} $$

We can use a similar procedure to prove that

$$\lim_{r\,\to\,0^+}\Im\int_{\color{#68009E}{\gamma_2}}f = -\frac{1}{4}\,.$$

Evaluating $\displaystyle \lim_{r\,\to\,0^+}\Im\int_{\color{#68009E}{\gamma_2}}f$, we get

$$ \begin{align} \lim_{r\,\to\,0^+}\Im\int_{\color{#68009E}{\gamma_2}}f &= \int_{r-1}^{-r}f(-it)d(-it) \\ &= \lim_{r\,\to\,0^+}\Im\int_{r-1}^{-r}\frac{e^{iy\left(-it\right)}}{e^{2\pi\left(-it\right)}-1}d\left(-it\right) \\ &= -\lim_{r\,\to\,0^+}\Re \int_{r-1}^{-r}\frac{e^{yt}}{e^{-2\pi it}-1}dt \\ &= \lim_{r\,\to\,0^+}\Re \int_{r-1}^{-r}e^{yt}\Re\left(\frac{1}{1-e^{-2\pi it}}\right)dt \\ &= \lim_{r\,\to\,0^+}\int_{r-1}^{-r}e^{yt}\Re\left(\frac{1}{2}-\frac{i}{2}\cot\left(\pi t\right)\right)dt \\ &= \lim_{r\,\to\,0^+}\int_{r-1}^{-r}\frac{e^{yt}}{2}dt \\ &= \frac{1}{2y}\left(1-\frac{1}{e^{y}}\right)\,. \\ \end{align} $$

Collecting our results together, we have

$$ \require{cancel}{0 = \int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dx + \cancelto{0}{\lim_{L\,\to\,\infty}\Im\int_{\color{#9E9300}{\lambda_2}}f}}-e^{-y}\int_{0}^{\infty}\frac{\sin\left(yt\right)}{e^{2\pi t}-1}dt-\frac{1}{4e^{y}}+\frac{1}{2y}\left(1-\frac{1}{e^{y}}\right)-\frac{1}{4} \\ $$ $$ \implies \bbox[10px,#F4FEFF]{\int_{0}^{\infty}\frac{\sin\left(yx\right)}{e^{2\pi x}-1}dx = \frac{1}{4}\coth\left(\frac{y}{2}\right)-\frac{1}{2y}\,.} $$

---

Going back to the double integral, $\mathcal{I}$ becomes

$$ \begin{align} \mathcal{I} &= -2i\int_{0}^{\infty}\frac{y}{e^{y}}\cdot\frac{1}{4}\left(\coth\left(\frac{y}{2}\right)-\frac{2}{y}\right)dy \\ &= i-\frac{i}{2}\int_{0}^{\infty}\frac{y}{e^{y}}\coth\left(\frac{y}{2}\right)dy\,. \end{align} $$

I'll leave it as an exercise (again) to prove that the remaining integral equals

$$\frac{\pi^{2}}{3}-1\,.$$

Other than that, we conclude with

$$ \bbox[15px,#FDFFF4,border:6px groove#9BB400]{\int_0^\infty\left(\frac1{(ti+1)^2(e^{2\pi t}-1)}-\frac1{(-ti+1)^2(e^{2\pi t}-1)}\right)dt = i\frac{9-\pi^{2}}{6}} $$

and we're done! $\blacksquare$