Your residue calculation looks correct, but like what the commenters Andrei and dan_fulea said, there are poles at all the integers and at $z = -a$, not just at $z=0$.
That being said, we will solve $(1)$ and $(2)$ by proving the following below.
$$
\bbox[15px,#EFF9FE,border:5px groove #FC189F ]{\oint_{\gamma}\frac{\cot(\pi z)}{(z+a)^2}dz = \begin{cases}
\displaystyle \sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2}\,, & -a \text{ is outside }\gamma \\
\displaystyle \sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2} - \frac{2\pi^2 i}{\sin^2 (\pi a)}\,, & -a \text{ is inside }\gamma\,
\end{cases}}
$$
$$
\bbox[15px,#EAFFF1 ,border:5px groove #07A1FF]{\lim_{n \to \infty}\oint_{\gamma}\frac{\cot(\pi z)}{(z+a)^2}dz = 0}
$$
Here, we define $\mathcal{P}$ as the set of poles $\left\{-n,-n+1,\ldots,n-1,n\right\}$, where $n$ is a positive integer, and $a \in \mathbb{C}\,\backslash\,(\gamma \cup \mathcal{P})$.
Foreword: There doesn't seem to be any restrictions on what $a$ should be. For this answer, I will suppose $-a$ is anywhere in the complex plane except on the integer points and the contour, which is likely the author's intention. I'm not sure the author intended on having $-a$ lie on the rectangular path, making $\gamma$ have an indent. I'll also mention a case where $a$ is an integer, albeit things get messy.
Here is a visual of what the contour looks like with the given function's domain coloring. Note that the domain coloring will vary depending on $-a$.
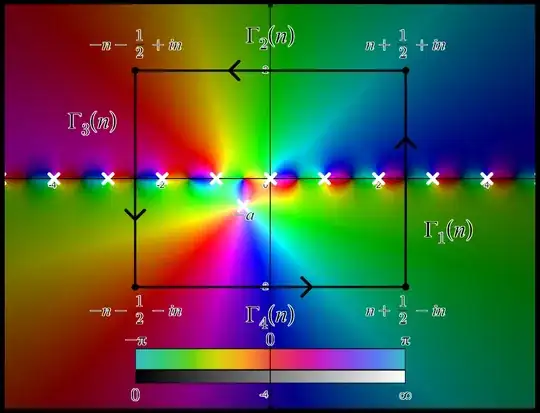
PROOF (1). We will do a proof by cases: one where $-a$ is outside the contour and the other where $-a$ is inside the contour.
CASE 1: POLE IS OUTSIDE THE BOX
Using Cauchy's Residue Theorem on the simple poles of $\mathcal{P}$, we have
$$
\begin{align}
\oint_{\gamma}\frac{\cot(\pi z)}{(z+a)^2}dz &= 2\pi i\sum_{k \in \mathcal{P}}\mathop{\mathrm{Res}}_{z=k}\frac{\cot(\pi z)}{(z+a)^2} \\
&= 2\pi i\sum_{k \in \mathcal{P}}\mathop{\mathrm{Res}}_{z=k}\frac{i\left(1+e^{2\pi iz}\right)}{\left(e^{\pi iz}-1\right)\left(e^{\pi iz}+1\right)\left(a+z\right)^{2}} \\
&= 2\pi i\sum_{k \in \mathcal{P}}\lim_{z\to k}\frac{i\left(1+e^{2\pi iz}\right)}{\frac{d}{dz}\left(e^{\pi iz}-1\right)\left(e^{\pi iz}+1\right)\left(a+z\right)^{2}} \\
&= 2\pi i\sum_{k \in \mathcal{P}}\lim_{z\to k}\frac{i\left(1+e^{2\pi iz}\right)}{2\left(a+z\right)\left(e^{2\pi iz}\left(1+\pi ai+\pi iz\right)-1\right)} \\
&= 2\pi i\sum_{k \in \mathcal{P}}\frac{i\left(1+e^{2\pi ik}\right)}{2\left(a+k\right)\left(e^{2\pi ik}\left(1+\pi ai+\pi ik\right)-1\right)} \\
&= \bbox[15px,#F9F6FF]{\sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2}\,.}
\end{align}
$$
CASE 2: POLE IS INSIDE THE BOX
For the second-order pole in the box, we evaluate the residue at that pole as follows:
$$
\begin{align}
2\pi i\mathop{\mathrm{Res}}_{z=-a}\frac{\cot\left(\pi z\right)}{\left(z+a\right)^{2}} &= 2\pi i \cdot \frac{1}{(2-1)!}\lim_{z\to-a}\frac{d^{2-1}}{dz^{2-1}}(z-(-a))^{2}\frac{\cot(\pi z)}{(z+a)^{2}} \\
&= 2\pi i \lim_{z \to -a} \frac{d}{dz} {(z+a)^2} \frac{\cot\left(\pi z\right)}{{\left(z+a\right)^{2}}} \\
&= 2\pi i \lim_{z\to -a} -\pi \csc^2 (\pi z) \\
&= -\frac{2\pi^2 i}{\sin^2(\pi a)}\,.
\end{align}
$$
We can use the answer from CASE 1 and get (by Cauchy's Residue Theorem again)
$$
\oint_{\gamma}\frac{\cot(\pi z)}{(z+a)^2}dz = \bbox[15px,#FFF6FA]{\sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2} -\frac{2\pi^2 i}{\sin^2(\pi a)}\,}
$$
and we're done with the first question!
PROOF (2): First, let $\gamma = \gamma(n)$ represent a sequence of rectangular contours such that $\gamma(n) = \Gamma_1(n) \cup \Gamma_2(n) \cup \Gamma_3(n) \cup \Gamma_4(n)$, shown in the cropped screenshot above. We construct a sequence of contour integrals $\displaystyle\oint_{\gamma(n)}f$ such that $\displaystyle\oint_{\gamma(n)}f$ converges as $n \to \infty$. Notice as the contour grows bigger, none of the integer poles ever touch it because, from the original problem, the contour has been judiciously chosen such that both $\Gamma_1(n)$ and $\Gamma_3(n)$ always lie directly in between two poles. A visual can be seen here on Desmos by playing with the slider $n$ I made. Since $a$ is not an element of $\gamma$ and is fixed, the contour eventually encloses $-a$ as it grows bigger, no matter how far $-a$ is from the origin.
Knowing this information, we can start solving the limit of the contour integral. We write
$$
\lim_{n\to\infty}\oint_{\gamma(n)}f(z)dz = \lim_{n\to\infty}\left(\int_{\Gamma_1(n)}f(z)dz + \int_{\Gamma_2(n)}f(z)dz + \int_{\Gamma_3(n)}f(z)dz + \int_{\Gamma_4(n)}f(z)dz\right)\,.
$$
Next, we have to evaluate those limits. (Evaluating those four limits would take a while.) As a demonstration, we can prove
$$
\lim_{n \to \infty} \int_{\Gamma_2(n)}f(z)dz = 0\,.
$$
Suppose $n > \max\left\{|\Re(a)|,|\Im(a)|\right\}$. Expressing the top line segment in set-builder notation, we have
$$
\Gamma_2(n) = \left\{-t+in\,:\, t\in \left[-n-\frac{1}{2},n+\frac{1}{2}\right]\right\}\,.
$$
We parameterize the contour integral with $z=-t + in$ so that the norm of $f$ is bounded above as shown here:
$$
\begin{align}
|f(z)| &= |f(-t+in)| \\
&= \frac{\left|\cot\left(\pi in-\pi t\right)\right|}{\left|-t+in+a\right|^{2}} \\
&=\frac{1}{\left|-t+in+a\right|^{2}}\cdot\left|\frac{e^{\pi it}e^{-\pi n}+e^{-\pi it}e^{\pi n}}{e^{\pi it}e^{-\pi n}-e^{-\pi it}e^{\pi n}}\right| \\
&\leq \frac{1}{\left|-t+in+a\right|^{2}}\cdot\left|\frac{e^{\pi n}+e^{-\pi n}}{e^{\pi n}-e^{-\pi n}}\right| \\
&= \frac{\left|\coth\left(\pi n\right)\right|}{\left|-t+in+a\right|^{2}} \\
&\leq \frac{\coth\pi}{\left|-t+in+a\right|^{2}} \\
&= \frac{\coth\pi}{(\Re(-t+in+a))^2+(\Im(-t+in+a))^2} \\
&= \frac{\coth\pi}{(\Re(a)-t)^2+(\Im(a)+n)^2} \\
&\leq \frac{\coth\pi}{(\Im(a)+n)^2}\,.\\
\end{align}
$$
For that last inequality, the denominator has a convenient lower bound $(\Im(a)+n)^2$ when $t = \Re(a)$.
Also, notice that the length of $\Gamma_2(n)$ is $2n+1$.
Using the Estimation Lemma and the Squeeze Theorem, we get
$$
\begin{align}
0 &\leq \left|\int_{\Gamma_2(n)}f(z)dz\right| \leq \frac{\coth\pi}{(\Im(a)+n)^2} \cdot (2n+1) \\
\lim_{n \to \infty} 0 &\leq \lim_{n \to \infty} \left|\int_{\Gamma_2(n)}f(z)dz\right| \leq \lim_{n \to \infty} \frac{\coth\pi}{(\Im(a)+n)^2} \cdot (2n+1) \\
0 &\leq \lim_{n \to \infty} \left|\int_{\Gamma_2(n)}f(z)dz\right| \leq 0 \text{ (because the bottom grows faster) }\\
\end{align}
$$
$$
\implies \lim_{n \to \infty} \left|\int_{\Gamma_2(n)}f(z)dz\right| = 0\,.
$$
Thus,
$$
\bbox[15px,#FFECEC]{\lim_{n \to \infty} \int_{\Gamma_2(n)}f(z)dz = 0\,.}
$$
The other Gamma integrals can be solved in a somewhat similar manner. Other than that, we are finally done! $\blacksquare$
MISCELLANEOUS THOUGHTS
Note that from CASE 2, we got
$$
\oint_{\gamma(n)}\frac{\cot(\pi z)}{(z+a)^2}dz = \sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2} -\frac{2\pi^2 i}{\sin^2(\pi a)}\,.
$$
Once you can prove that $\displaystyle \lim_{n \to \infty}\oint_{\gamma(n)} \frac{\cot(\pi z)}{(z+a)^2}dz = 0$, you can refer to the answer right above and get the consequence
$$
\bbox[15px,border:5px groove #00949C]{\sum_{n=-\infty}^{\infty} \frac{1}{(a+k)^2} = \frac{\pi^2}{\sin^2(\pi a)}}
$$
when $a$ is not an integer.
If $-a$ were to be an integer stuck inside $\gamma$, the calculations get really messy. To simplify some of the grunt work, we can express $f(z)$ as a Laurent asymptotic expansion to help calculate the third order pole at $z=-a$, shown here,
$$
\begin{align}
2\pi i\mathop{\mathrm{Res}}_{z=-a}f(z) &= 2\pi i\mathop{\mathrm{Res}}_{z=-a}\left(\frac{1}{\pi\left(z+a\right)^{3}}-\frac{\pi}{3\left(z+a\right)}-\frac{\pi^{3}}{45}\left(z+a\right)-\frac{2\pi^{5}}{945}\left(z+a\right)^{3}+O\left(\left(z+a\right)^{5}\right)\right)\,,
\end{align}
$$
and get the residue to equal $\displaystyle -\frac{\pi}{3}$. This results in
$$
\oint_{\gamma}\frac{\cot(\pi z)}{(z+a)^2}dz = \sum_{k \in \mathcal{P}} \frac{2i}{(a+k)^2} - \frac{2\pi^2 i}{3}\,.
$$
I don't know if there is a closed form for that expression when $n \to \infty$. :P
