a full proof for the Fundamental Theorem of affine geometry

Question

Let $n\geq 2$ and a bijection $T:\ \mathbb R^n\longrightarrow\mathbb R^n$ satisfies $\ T(0)=0\,$ and $\,T$ maps straight lines to straight lines.

Then $T$ is a linear map.

My proof :

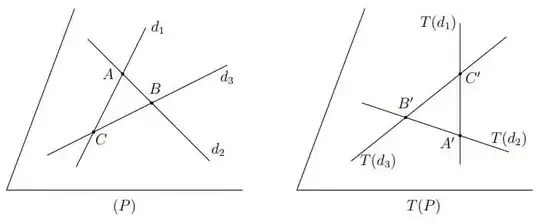
Let $(P)\subset\mathbb R^n$ be a 2-plane and the straight lines $d_1,d_2,d_3\subset(P)$ which intersect pairwise respectively at $A,B,C$. Since $T$ is bijective and $T(d_1),T(d_2),T(d_3)$ are straight lines, they intersect pairwise respectively at $T(A)=A',\,T(B)=B',\,T(C)=C'$. Hence they form a 2-plane $(A'B'C')$.

For each straight line $d\subset (P)$, if $d$ doesn't contain $A,B,C$ then $d$ must intersect with at least 2 lines of $d_1,d_2,d_3$ at at least 2 points. Since $T$ is bijective, so is $T(d)$. Hence, $T(d)\subset (A'B'C')$. We conclude $T(P)\subseteq(A'B'C')$. By a similar deduce, we show that $T^{-1}(A'B'C')\subseteq(P)$, therefore $T(P)=(A'B'C')$.

Let $d,d'\subset(P)$ be 2 distinguish parallel lines. Since $T(d)\cap T(d')=\varnothing$ and $T(d),T(d')\subset T(P)$, we have $T(d), T(d')$ are parallel. Thus, if $A,B,C,D$ are the vertices of the parallelogram $ABCD$, then $A',B',C',D'$ must be the vertices of the parallelogram $A'B'C'D'$.

Let $u,v\in\mathbb R^n\setminus{0}$ be linearly independent. Since $0,u,u+v,v$ be the vertices of a parallelogram, so do $0,T(u),T(u+v),T(v)$, this implies $T(u+v)=T(u)+T(v)$.

Let $\mu,\lambda\in\mathbb R\setminus\{0\}$ and $u,v\in \mathbb R^n\setminus\{0\}$ be linearly independent. Then $\{\mu u,v\},\, \{\lambda u,\mu u+v\},\, \{\lambda u+\mu u,v\}$ are also linearly independent. Thus, \begin{align} T(\lambda u)+T(\mu u)+T(v)\,&=\,T(\lambda u)+T\big(\mu u+v\big) \\ &=\,T\big(\lambda u+\mu u+v\big) \\ &=\,T\big(\lambda u+\mu u\big)+T(v),\tag1 \end{align} which implies $T\big(\lambda u+\mu u\big)=T(\lambda u)+T(\mu u)$. So, $T$ is additive.

Given $0\ne u\in\mathbb R^n$. Because $\langle u\rangle$ is a straight line, $T(\langle u\rangle)$ is also straight line. In the other hand, $\big<T(u) \big>$ is also a straight line, and both $T(\langle u\rangle),\,\big<T(u) \big>$ contain $0, T(u)$, therefore $T(\langle u\rangle)=\big<T(u) \big>$. We deduce \begin{align} \forall\lambda\in\mathbb R,\ \exists\,\mu(u,\lambda)\in\mathbb R:\ T(\lambda u)=\mu(u,\lambda) T(u).\tag2 \end{align} Given $\lambda,\varepsilon\in\mathbb R\setminus\{0\}$ and $u,v\in \mathbb R^n\setminus\{0\}$ be linearly independent. We have the straight lines $\big[u,v\big]$ and $\big[\lambda u,\lambda v \big]$ are parallel, and the straight lines $\big[\varepsilon u,v\big]$ and $\big[\lambda\varepsilon u,\lambda v \big]$ are parallel. Hence, $\big[T(u),T(v)\big]$ and $\big[T(\lambda u),T(\lambda v)\big]$ are parallel, and $\big[T(\varepsilon u),T(v)\big]$ and $\big[T(\lambda\varepsilon u),T(\lambda v)\big]$ are also parallel. By Thales's Theorem, we have \begin{align} \frac{\big\|T(\lambda u)\big \|}{\big\|T(u) \big\|}=\frac{\big\|T(\lambda v)\big \|}{\big\|T(v) \big\|}=\frac{\big\|T(\lambda\varepsilon u)\big \|}{\big\|T(\varepsilon u) \big\|},\tag3 \end{align} thus \begin{align} \big|\mu(u,\lambda)\big|\,=\,\big|\mu(\varepsilon u,\lambda) \big|\tag4 \end{align} or \begin{align} \mu(u,\lambda)\,=\,\pm\mu(\varepsilon u,\lambda).\tag5 \end{align}

Now, we have \begin{align} \mu(u,\lambda\varepsilon)T(u)\,=\,T(\lambda\varepsilon u)\,=\,\mu(\varepsilon u,\lambda)\mu(u,\varepsilon)T(u)\tag6 \end{align} thus \begin{align} \mu(u,\lambda\varepsilon)\,=\,\mu(\varepsilon u,\lambda)\mu(u,\varepsilon)\,=\,\pm\mu(u,\lambda)\mu(u,\varepsilon)\tag7 \end{align}

We also have \begin{align} \mu\big(u,\lambda+\varepsilon\big)T(u)\,&=\,T\big((\lambda+\varepsilon)u \big) \\ &=\,T(\lambda u)+T(\varepsilon u) \\ &=\, \big[\mu(u,\lambda)+\mu(u,\varepsilon)\big] T(u)\tag8 \end{align} hence $\mu\big(u,\lambda+\varepsilon\big)=\mu(u,\lambda)+\mu(u,\varepsilon)$.

We are so close to show that $\mu(u,\cdot)$ is a field automorphism of $\mathbb R$. And a well known result states that the only field automorphism of $\mathbb R$ is the identity map, therefore $\mu(u,\cdot)=id$. This will complete our lengthy proof. But, my final impedent, how to show that $\mu(u,\lambda\varepsilon)=\mu(u,\lambda)\mu(u,\varepsilon)$, which means to show that the negative case is no true ? Since I have tried and can't find out any contradiction for this case.

May anyone give me some helps ? If you get another fascinating proof for this Theorem, like using calculus and try showing $T$ is continuous some way for instance, feel free to share your great idea. Thanks.

Answer 1

The part of the proof where you use the Thales theorem should also give you the sign.

If $[T(u), T(v)]$ and $[T(\lambda u), T(\lambda v)]$ are parallel, then not only $\frac{\| T(\lambda u) \|}{\| T(u) \|} = \frac{\|T(\lambda v)\|}{\|T(v)\|}$, but also $T(\lambda u)$ and $T(\lambda v)$ lie at the same side of the line $[T(u), T(v)]$. In terms of $\mu$ this means not only $|\mu(u,\lambda)| = |\mu(v, \lambda)|$, but $\mu(u,\lambda) = \mu(v, \lambda)$.